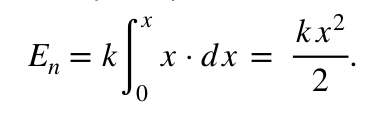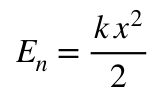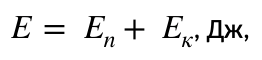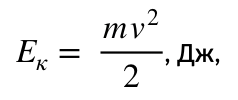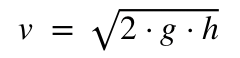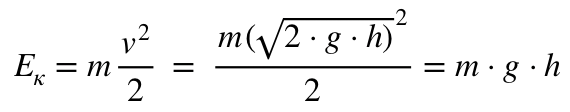Кинетическая энергия груза на пружине формула

Потенциальная энергия пружины и кинетическая – что это, какая формула?

Во многих механизмах используется потенциальная и кинетическая энергия пружины. Их используют для выполнения различных действий. В отдельных узлах они фиксируют детали в определенном положении, не позволяя смещать в какую-либо сторону (барабан револьвера относительно корпуса). Другие пружинные системы возвращают исполнительный механизм в исходное положение (курок ручного огнестрельного оружия). Есть устройства, где узлы с гибкими свойствами совершают перемещения в устойчивое положение (механические стабилизаторы).

Работа связана с изменением геометрических параметров упругого тела. Прилагая нагрузку, заставляют эластичную деталь сжиматься (растягиваться или изгибаться). При этом наблюдается запасание энергии. Возвратное действие сопровождается набором скорости. Попутно возрастает кинетическая энергия.

Потенциальная энергия пружины

Рассматривая в качестве накопителя энергии пружину, следует отметить ее отличительные свойства от иных физических тел, которые могут накапливать энергетический потенциал. Традиционно понимается следующее: для накопления потенциала для последующего движения необходимо совершение движения в силовом поле:

Е_п = F ⋅ l, Дж (Н·м),

где Е_п– потенциальная энергия положения, Дж;
F – сила, действующая на тело, Н;
l – величина перемещения в силовом поле, м.

Энергия (работа) измеряются в Джоулях. Величина представляет произведение силы (Н) на величину перемещения (м).

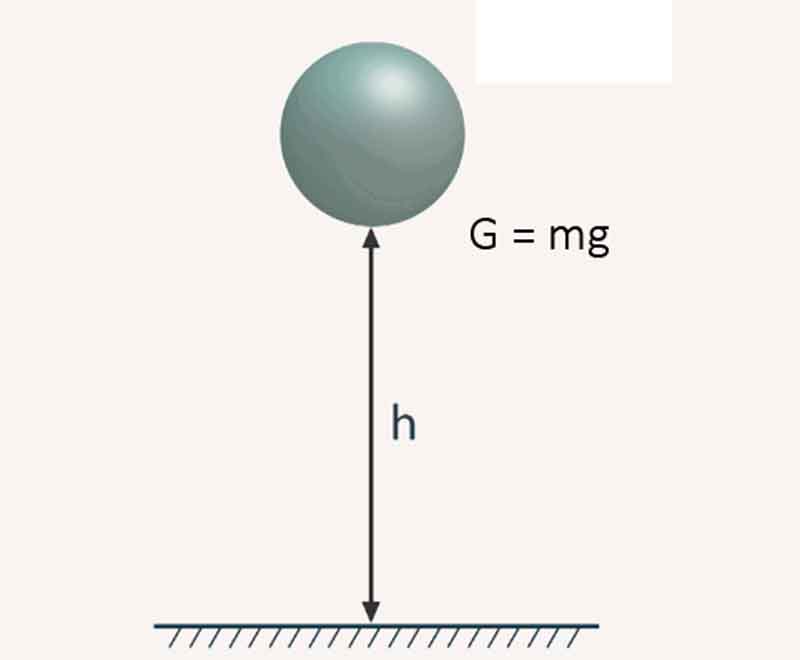
Если рассматривать условие в поле тяготения, то величина силы находится произведением ускорения свободного падения на массу. Здесь сила веса находится с учетом g:

Е_п = G ⋅ h = m ⋅ g ⋅ h, Дж

здесь G – вес тела, Н;
m – масса тела, кг;
g – ускорение свободного падения. На Земле эта величина составляет g = 9,81 м/с².

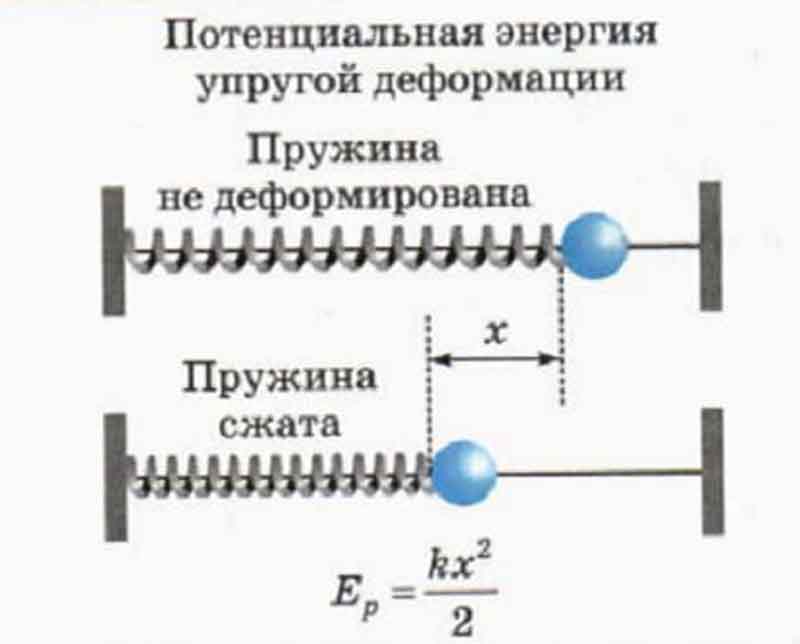
Если расстраивается пружина, то силу F нужно определять, как величину, пропорциональную перемещению:

где k – модуль упругости, Н/м;
х – перемещение при сжатии, м.

Величина сжатия может изменяться по величине, поэтому математики предложили анализировать подобные явления с помощью бесконечно малых величин (dx) .

При наличии непостоянной силы, зависящей от перемещения, дифференциальное уравнение запишется в виде:

dE_п = k ⋅ x ⋅ dx

здесь dE_п – элементарная работа, Дж;
dx – элементарное приращение сжатия, Н.

Интегральное уравнение на конечном перемещении запишется в виде. Ниже вывод формулы:

Пределами интегрирования является интервал от до х. Деформированная пружина приобретает запас по энергетическим показателям

Окончательно формула для расчета величины потенциальной энергии сжатия (растягивания или изгиба) пружины запишется формулой:

Закон сохранения механической энергии

Закон сохранения энергии существует независимо от желания наблюдателя. Все физические законы имеют статистический характер: существуют только подтверждения их выполнения, нет ни одного адекватно выполненного опыта, при котором наблюдается нарушение этой закономерности. Природные явления только подтверждают сохранность работы и энергозатрат, затраченных на ее выполнение.

На основании изложенного сформулировано положение:

где Е_к – кинетическая энергия, Дж.

Рассматривая перемещения тела, наблюдаются изменения потенциальной и кинетической энергий. При этом сумма значений остается постоянной.

Проще всего проследить за изменениями между разными видами энергетических показателей при рассмотрении движения маятника.

Из крайнего положения (шарик на нити отклонился в одну из сторон, Еп = max) тело движется под действием силы тяжести. При этом снижается запасенная энергия. Движение сопровождается увеличением скорости. Поэтому нарастают показатели динамического перемещения Е_к.

В нижней точке не остается никаких запасенных эффектов от положения шарика. Он опустился да минимума. Теперь Е_к =max.

Поучается, при совершении гармонических колебаний маятник поочередно накапливает то один, то другой вид энергии. Механические превращения из одного вида в другой налицо.

Кинетическая энергия

Движущееся тело характеризуется скалярной величиной (масса) и векторная величина (скорость). Если рассматривать реальное перемещение в пространстве, то можно записать уравнение для определения кинетической энергии:

здесь v – скорость движения тела, м/с.

Использование кинетического преобразования можно наблюдать при колке орехов.

Приподняв камень повыше, далекие предки создавали необходимый потенциал для тяжелого тела.

Приподняв камень на максимальную высоту, разрешают ему свободно падать.

Двигаясь с высоты h, он набирает скорость

Поэтому в конце падения будет получена кинетическая энергия

Рассматривая входящие величины, можно увидеть, как происходит преобразование величин. В конце получается расчетная формула для определения потенциальной энергии.

Даже на уровне вывода зависимостей можно наблюдать выполнение закона сохранения энергии твердого тела.

Использование энергии пружины на практике

Явление преобразования потенциальной энергии пружины в кинетическую используется при стрельбе из лука.

Натягивая тетиву, стреле сообщается потенциал для последующего движения. Чем жестче лук, а также ход при натягивании тетивы, тем выше будет запасенная энергия. Распрямляясь дуги этого оружия, придадут метательному снаряду значительную скорость.

В результате стрела полетит в цель. Ее поражающие свойства определятся величиной кинетической энергии (mv²/2).

Для гашения колебаний, возникающих при движении автомобиля, используют амортизаторы. Основным элементом, воспринимающим вертикальную нагрузку, являются пружины. Они сжимаются, а потом возвращают энергию кузову. В результате заметно снижается ударное воздействие. Дополнительно устанавливается гидроцилиндр, он снижает скорость обратного движения.

Рассмотренные явления используют при проектировании механизмов и устройств для автоматизации процессов в разных отраслях промышленности.

Колебания груза на пружине — формулы, уравнения и задачи

Теория периодичности относится к общей физике. Повторяемость некоторых процессов в течение времени определяют с помощью различных величин, например, угла, напряжённости, температуры. Для изучения явления удобно использовать маятник. Одним из его видов является пружина с грузом. Колебания в такой системе зависят от периода, частоты и амплитуды. Узнать эти параметры можно, зная начальные условия и уравнения, описывающие механическую работу.

Общие сведения

Колебания — это изменения какой-либо величины в точности или приблизительно повторяющиеся во времени. Если рассматривать процесс, с точки зрения механики, то он описывается положением тела. Повторение в точности является периодическим. Математически это можно записать формулой: x (t + T) = x (t), где T — время, в течение которого совершается одно полное колебание (период). Число циклов принято обозначать буквой N. Его находят как отношение времени к периоду: N = t / T.

При исследовании процесса не всегда бывает удобно оперировать временем, поэтому часто используют число колебаний за единицу времени. Эта величина называется частотой. Находят её количество по формуле: f = 1 / T. Доказать справедливость приведённого равенства просто. Число колебаний зависит от времени и частоты: N = f * t. Отсюда: f = N / t = (t / T) / t = 1 / T.

Очень важно не только понимать суть характеристик колебания, но и знать единицы его измерения. Вот основные из них:

период — секунды (с);
частота — герцы (Гц);
число колебаний — безразмерная величина.

Если в течение времени меняется и координата, то периодически будет изменяться и скорость. Значит: vx (t + T) = Vx (t).

Исходя из верности равенства, можно сказать, что условие периодичности будет справедливо и для проекции, то есть изменения ускорения. Отсюда следует, что сила действующая на тело тоже будет переменной: Fx (t + T) = Fx (t).

При процессе также происходит изменение потенциальной и кинетической энергий. Действительно, так как в процессе колебания скорость не является постоянной величиной, то соответственно будет меняться кинетическая работа. Потенциальная же энергия зависит от координат. Например, если рассмотреть период колебаний пружинного маятника, то за это время тело переместится из нижнего положения в верхнее и вернётся обратно. Значит, координата физического объекта изменится от нуля до какого-то граничного значения.

Следует отметить, что периодичные движения обязательно будут происходить в той системе, в которой есть положение равновесия. Причём оно должно быть устойчивым. То есть существует равнодействующая сила, стремящаяся привести объект в положение, соответствующее покою. Поэтому для поддержания отклонений нужна дополнительная сила. Колебательную систему (осциллятор) под действием вынужденной периодической силы называют вынужденной.

Пружинный маятник

Это устройство является простейшим примером свободных колебаний. В его состав входит кронштейн, пружина и груз. В качестве последнего может выступать любое физическое тело. Масса пружины по сравнению с грузом считается малой и при исследованиях не учитывается.

При изучении такой системы важной задачей является измерение периода движения тела, подвешенного к пружине. Определение понятию пружинного маятника, которое даётся в учебниках по физике довольно обобщённое. Считается, что это конструкция, в которой тело, имеющее массу m, подвешено на упругой пружине обладающей жёсткостью K. При этом из состояния равновесия систему может вывести упругая сила F = — k * x, где: x- расстояние от середины пружинного элемента до поверхности прикреплённого к нему груза.

Можно выделить два достаточных условия возникновения свободных колебаний:

Суть изучения гармонических колебаний состоит в определении их частоты движения или периода. В пружинном маятнике, впрочем, как и в любой колебательной системе, параметры зависят от ряда характеристик. Из основных величин, описывающих процесс, можно выделить: массу груза и жёсткость. Поэтому задача и состоит в выяснении, как период зависит от этих двух параметров.

Во время экспериментов регулировать массу довольно легко. Для этого можно взять эталонные гири и, соединяя их, увеличивать вес. Жёсткость же пружины можно изменить, добавляя параллельно или последовательно к ней другое сжимающееся тело. Чтобы выяснить, как будет изменяться характеристика растягивающегося элемента, нужно знать, что же представляет собой параметр. Так, под жёсткостью тела понимают отношение силы упругости к удлинению: k0 = F / Δ L. Измеряется величина в ньютонах, делённых на метр (Н/м).

Исходя из правила, если соединить две пружины параллельно и деформировать их, то можно утверждать, что первый и второй элемент растянется на одинаковую длину ΔL. Значит, возникнет две одинаково направленных силы упругости. Отсюда равнодействующая будет равняться: K = 2F/ ΔL = 2k0. Для последовательного же соединения длина всей системы увеличится на 2 ΔL. Сила упругости будет равна F. Соответственно, жёсткость будет изменяться по формуле: K = F / 2ΔL = k0 / 2.

Зависимость периода

При проведении эксперимента можно исследовать пять различных комбинаций поведения груза на пружине — два варианта связаны с весом и три с жёсткостью. Чтобы выполнить опыт самостоятельно нужно будет взять вертикальный кронштейн, две одинаковые пружины и два равных по весу груза. Так как в реальности период будет довольно маленький, то для его измерения можно взять время, например, пятидесяти колебаний, а потом полученный результат разделить на это число. Подсчёт времени удобно выполнять с помощью секундомера.

Вычисленные результаты нужно занести в таблицу. Примерный порядок чисел должен получиться таким:

k m	m0	2m0
k0 / 2	0,68	0,93
k0	0,46	0,64
2k0	0.34	0,47

Эти данные можно проанализировать. Выводы будут следующими:

с ростом массы физического тела период цикличности увеличивается;
по мере увеличения жёсткости период колебаний уменьшается.

Приведённые утверждения, возможно, описать и количественно. Исходя из результатов, величины, стоящие в ячейке m0k0 и 2m02ko почти совпадают. С точки зрения физики, так и должно быть. Если взять грузик на пружине и измерить характеристику, а потом добавить к нему точно такую же систему, то период не поменяется. Это и можно наблюдать во время опыта. Значит, период движения зависит от того каким будет отношение массы к жёсткости.

По аналогии можно рассмотреть, как влияет жёсткость. Из эксперимента, видно, что если её увеличить дважды на одну и ту же величину, то она возрастёт в четыре раза, а значение обратное частоте уменьшится на это же число. Отсюда можно предположить, что период будет обратно пропорционален корню квадратному из жёсткости.

Объединив эти две гипотезы можно сделать заключение. Что период амплитуды колебаний груза на пружине будет прямо пропорционален корню квадратного из отношения массы к жёсткости: T = √(m / k). Проверить это утверждение можно по теории размерности. Подставив в формулу единицы измерения, получим: √(m / k) = √(кг / (Н/м)) = √(кг * м / Н). Учитывая, что ньютон — это отношение метра к секунде в квадрате или килограмму, умноженному на метр и делённому на секунду, размерное равенство примет вид: √(кг * м/Н) = √(c 2 * м/м) = √с 2 = с.

Для написания полной формулы в равенство нужно вести ещё коэффициент. Он будет равняться 2p. Значит, период колебаний пружинного маятника количественно описывается выражением: T = 2p * √ (m / k).

Примеры решения задач

Практические задания помогают лучше разобраться в теоретическом материале и запомнить нужные для решения формулы. Существуют различные примеры, с помощью которых можно довольно быстро проработать весь изученный курс. Вот два задания с подробным описанием решения на вычисления параметров пружинных колебаний тела. Разобравшись в них, можно переходить к самостоятельному вычислению более сложных примеров.

Задание № 1. Груз, подвешенный к пружине, перемещается циклически по вертикальной оси. За восемь секунд он совершил тридцать два колебания. Определить частоту. Итак, по условию задания дано время t = 8 c и число полного перемещения тела N = 32. Чтобы решить эту задачу нужно воспользоваться формулой нахождения периода: T = t / N. Все величины для этого есть: T = 8 c / 32 = 1 / 4 = 0,25 секунды. Частота связана с периодом выражением: f = 1 / T. После подстановки чисел получится ответ равный четырём герцам.

Задание № 2. Грузик совершает колебания на пружине с жёсткостью сто ньютон на метр. При этом максимальная скорость движения составляет два метра в секунду. Вычислить массу тела учитывая, что максимальная амплитуда отклонения от точки покоя составляет десять сантиметров. Силой трения пренебречь.

При решении примера нужно рассуждать следующим образом. Когда будет максимальное растяжение пружины, то скорость груза равна нулю: V1 = 0. Значит, кинетическая энергия тоже будет нулевой: Ek1 = 0.

В этот момент останется только потенциальная энергия вытянутой пружины Ep1. В положении равновесия скорость тела максимальная и равняется V = 2 м/с. Так как пружина в этот момент нерастянута и несжатая, то Ep = 0.

По закону сохранения энергии: Ek1 + Ep1 = Ek + Ep. Кинетическая работа при растянутой пружине равняется нулю, так же как и потенциальная в состоянии покоя, значит, Ep1 = (k * L 2 ) / 2, где L — удлинение, а k — жёсткость. Энергию же можно найти так: Ek = mV 2 / 2. Так как тело совершает колебания около положения равновесия, то вытянутость пружины будет равняться амплитуде.

Перед тем как непосредственно переходить к составлению итоговой формулы и вычислениям необходимо все значения измерений привести в соответствии с СИ. Так, амплитуда указана в сантиметрах, поэтому её нужно перевести в метры. Теперь можно переходить к составлению отношения и подстановки данных: (k * L 2 ) / 2 = mV 2 / 2. Отсюда: m = (k * L) / V 2 = (100 Н/м * 0,1 2 м) / 2 2 м/с = 1 / 4 = 0,25 килограмма.

ИНФОФИЗ — мой мир.

Надеюсь, данный раздел поможет Вам эффективно и интересно изучать физику.

Учите физику!

Как сказал.

Если вы студент, значит перед вами стоит тысяча возможностей. Найдите в себе силы, чтобы использовать хотя бы одну из них.

Вопросы к экзамену

Для всех групп технического профиля

Законы и формулы

Я учу детей тому, как надо учиться

Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.

Новости и знаменательные даты

13. Вопросы к зачету по теме: «Колебания и волны»

Печать
E-mail

Вопросы для подготовки к зачету по теме: «Колебания и волны»

11. Механические колебания. Параметры колебательного движения. Уравнение гармонического колебания.

12. Математический и пружинный маятники. Периоды их колебаний. Превращение энергии при механических колебаниях.

13. Механические волны. Поперечные и продольные волны. Понятие фронта и длины волны.

38. Свободные электромагнитные колебания в колебательном контуре. Формула Томсона.

39. Электромагнитное поле и его распространение в пространстве в виде электромагнитных волн

40. Переменный ток, его получение и параметры. Уравнение переменного тока.

41. Действующие значения переменного тока и напряжения.

42. Активное, индуктивное и емкостное сопротивление в цепи переменного тока. Закон Ома для цепи переменного тока.

43. Устройство и принцип действия однофазного трансформатора.

Ответы.

Часть 1. Основные физические величины, единицы их измерения, формулы для нахождения.

Часть 2. Основные понятия.

Механические колебания – это движения, которые точно или приблизительно повторяются через одинаковые промежутки времени.

Смещение х – отклонение колеблющейся точки от положения равновесия. Единица измерения – 1 метр.

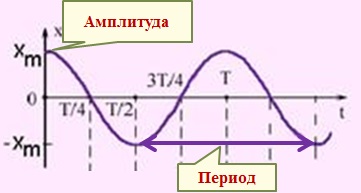
Амплитуда колебаний А – максимальноеотклонение колеблющейся точки от положения равновесия. Единица измерения – 1 метр.

Период колебаний T – минимальный интервал времени, за который происходит одно полное колебание, называется. Единица измерения – 1 секунда.

где t — время колебаний, N — количество колебаний, совершенных за это время.

По графику гармоническихколебаний можно определить период и амплитуду колебаний:

Частота колебаний ν – физическая величина, равная числу колебаний за единицу времени, показывает, сколько колебаний совершается за 1 с.Единица частоты – герц (Гц).

Частота – величина, обратная периоду колебаний:

Циклическая частота ω – число колебаний за 2π секунды.

Частота колебаний ν связана с циклической частотой ω и периодом колебаний T соотношениями:

Фаза гармонического процесса – величина, стоящая под знаком синуса или косинуса в уравнении гармонических колебаний φ = ωt + φ. При t = 0 φ = φ, поэтому φ называют начальной фазой.

Простейшим видом колебательного процесса являются простые гармонические колебания, которые описываются уравнением

x = x_m cos (ωt + φ)

x – смещение тела от положения равновесия

x_m – амплитуда колебаний, то есть максимальное смещение от положения равновесия

ω – циклическая или круговая частота колебаний

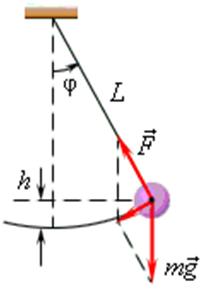
Математический маятник — это тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела.

Период колебаний математического маятника:

Период колебаний математического маятника зависит отдлины нити и от ускорения свободного падения той местности, где установлен маятник.

При гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот. Если в колебательной системе отсутствует трение, то полная механическая энергия при механических колебаниях остается неизменной.

Для математического маятника полная механическая энергия равна:

При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия равны нулю. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. В положении максимального отклонения полная энергия математического мятника равна потенциальной энергии тела, поднятого на высоту h:

Здесь h_m – максимальная высота подъема маятника в поле тяготения Земли.

Когда тело при своем движении проходит через положение равновесия, его скорость максимальна, значит, в этот момент оно обладает максимальной кинетической энергией. Тело находится на высоте нулевого уровня, значит, в этот момент оно обладает нулевой потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии.

При прохождении положения равновесия полная энергия равна кинетической энергии тела:

Тело проскакивает положение равновесия по закону инерции. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.

Здесь x_m – максимальное значение отклонения маятника от положения равновесия, v _m – максимальное значение его скорости.

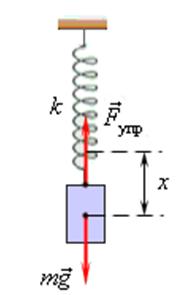
Пружинный маятник — это груз некоторой массы m, прикрепленный к пружине жесткости k, второй конец которой закреплен неподвижно.

Период T гармонических колебаний груза на пружине равен

Период колебаний пружинного маятника зависит от массы груза и от жесткости пружины.

Для пружинного маятника полная механическая энергия равна:

При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на пружине потенциальная энергия – это энергия упругих деформаций пружины, поэтому в положении максимального отклонения полная энергия мятника равна потенциальной энергии деформированной пружины:

Когда тело при своем движении проходит через положение равновесия, его скорость максимальна, значит, в этот момент оно обладает максимальной кинетической. Пружина при этом не деформирована, значит, в этот момент тело обладает нулевой потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии.

При прохождении положения равновесия полная энергия равна кинетической энергии груза: