Число зубьев шестерни таблица

Модуль зубьев зубчатого колеса

Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.

Что такое модуль зубчатого колеса

Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров

• диаметр;
• число зубьев;
• шаг;
• высота зубца;
• и некоторые другие.

Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.

В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.

Для расчета этого параметра применяют следующие формулы:

Параметры зубчатых колес

Модуль зубчатого колеса можно рассчитать и следующим образом:

где h — высота зубца.

где De — диаметр окружности выступов,а z — число зубьев.

Что же такое модуль шестерни?

это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

проведя преобразование, получим:

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов D_e получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

Диаметр окружности впадин D_i соответствует D_e за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

что соответствует формуле:

и если выполнить подстановку, то получим:

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s_в, получаем формулы для ширины впадины

• для отлитых зубцов: s_в=πm-1,53m=1,61m:
• для выполненных путем фрезерования- s_в= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Исходные данные и замеры

На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.

Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.

Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.

Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.

Результаты расчетов

Для более крупных потребуются измерения и вычисления.

Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:

Последовательность действий следующая:

• измерить диаметр штангенциркулем;
• сосчитать зубцы;
• разделить диаметр на z+2;
• округлить результат до ближайшего целого числа.

Зубец колеса и его параметры

Данный метод подходит как для прямозубых колес, так и для косозубых.

Расчет параметров колеса и шестерни косозубой передачи

Расчетные формулы для важнейших характеристик шестерни косозубой передачи совпадают с формулами для прямозубой. Существенные различия возникают лишь при прочностных расчетах.

Виды зубчатых колес, шестерен

Обычно шестерни имеют профиль зубьев с эвольвентной боковой формой. Так как эвольвентное зацепление имеет ряд преимуществ перед остальными: форма этих зубьев соответствует условиям их прочности, зубья легко изготовить и обработать, шестерни не чувствительны к точности установки. Тем не менее, существуют зубчатые передачи с циклоидальной формой профиля зубьев, а так же с шестернями с круговой формой профиля зубьев, например — передача Новикова. Помимо этого, применяется несимметричный профиль зуба, например в храповых механизмах.

Параметры эвольвентной шестерни:

Модуль шестерни (m) – это основной параметр, который определяется из прочностного расчёта зубчатых передач. Чем сильнее нагрузка на передачу, тем больше значение модуля, единица измерения модуля – миллиметры.

Расчет модуля шестерни:

d — диаметр делительной окружности

z — число зубьев шестерни

p — шаг зубьев

d_a — диаметр окружности вершин темной шестерни

d_b — диаметр основной окружности — эвольвенты

d_f — диаметр окружности впадин темной шестерни

h_aP+h_fP — высота зуба темной шестерни, x+h_aP+h_fP — высота зуба светлой шестерни

В машиностроении приняты стандартные значения модуля зубчатого колеса для удобства изготовления и замены зубчатых колёс, представляющие собой числа от 1 до 50.

Высота головки зуба — h_aP и высота ножки зуба — h_fP в случае, так называемого, «нулевого» зубчатого колеса соотносятся с модулем m следующим образом: h_aP = m; h_fP = 1,2 m, то есть:

Отсюда получаем, что высота зуба h = 2,2m

Так же можно практически вычислить модуль шестерни, при этом, не имея всех данных для определения модуля, по следующей формуле:

Продольная линия зуба

Прямозубые шестерни

Прямозубые шестерни — самый применяемый тип зубчатых колёс. Зубья расположены в радиальных плоскостях, линия контакта зубьев пары зубчатых колес параллельна оси вращения, как и оси обеих зубчатых колес (шестеренок) располагаются строго параллельно.

Косозубые шестерни

Косозубые шестерни – это модернизированная версия прямозубых шестерен. Зубья, в таком случае, расположены под углом к оси вращения. Зацепление зубьев этих шестерен происходит тише и плавнее, чем у прямозубых. Они применяются либо в малошумных механизмах, либо в тех которые требуют передачи большого крутящего момента на больших скоростях. К недостаткам этого типа шестерен можно отнести: увеличенную площадь соприкосновения зубьев, что вызывает значительное трение и нагрев деталей, а вследствие: потеря мощности и дополнительное использование смазочных материалов; так же механическая сила, направленная вдоль оси шестеренки, вынуждает применять упорные подшипники для установки вала.

Шевронные колёса

Шевронные шестерни решают проблему механической осевой силы, которая возникает в случае применения косозубых колес, так как зубья шевронных (елочных) колёс изготавливаются в виде буквы «V» (или же они образовываются стыковкой двух косозубых колёс со встречным расположением зубьев). Осевые механические силы обеих половин шевронной шестерни взаимно компенсируются, поэтому нет нет необходимости использования упорных подшипников для установки валов. Шевронная передача является самоустанавливающейся в осевом направлении, в следствии чего, в редукторах с шевронными колесами один из валов устанавливают на подшипниках с короткими цилиндрическими роликами — плавающих опорах.

Шестерни с внутренним зацеплением

Шестерни такого типа имеют зубья, нарезанные с внутренней стороны. При их использовании происходит одностороннее вращение ведущей и ведомой шестерен. В данной зубчатой передаче меньше затрат на трение, а значит выше КПД. Применяются зубчатые колеса с внутренним зацеплением в ограниченных по габаритам механизмах, в планетарных передачах, в шестеренных насосах, в приводе башни танка.

Винтовые шестерни

Шестерни имеют форму цилиндра с расположенными на нем зубьями по винтовой линии. Эти шестеренки используются на непересекающихся валах, которые располагаются перпендикулярно друг друга, угол между ними 90°.

Секторные шестерни

Секторная шестерня – это часть (сектор) шестерни любого типа, она позволяет сэкономить в габаритах полноценной шестерни, так как применяется в передачах, где не требуется вращение этого зубчатого колеса (шестеренки) на полный оборот.

Шестерни с круговыми зубьями

Шестерни этого типа имеют линию зубьев в виде окружности радиуса, за счет этого контакт в передаче происходит в одной точке на линии зацепления, которая располагается параллельно осям шестерен. Передачи с круговыми зубьями «Передача Новикова» имеет лучшие ходовые качества, чем косозубые – высокую плавность хода и бесшумность, высокую нагрузочную способность зацепления, но при одинаковых условиях их ресурс работы и КПД ниже, к прочему изготовление этих шестерен значительно сложнее. Поэтому применение таких шестеренок ограниченно.

Конические шестерни

Конические шестерни имеют различные виды, отличаются они по форме линий зубьев, с прямыми, с криволинейными, с тангенциальными, с круговыми зубьями. Применяются конические зубчатые передачи в машинах для движения механизма, где требуется передать вращение с одного вала на другой, оси которых пересекаются. Например, в автомобильных дифференциалах, для передачи момента от двигателя к колесам.

Зубчатая рейка

Зубчатая рейка является частью зубчатого колеса с бесконечным радиусом делительной окружности. Вследствие этого ее окружности представляют собой прямые параллельные линии. Эвольвентный профиль зубчатой рейки тоже имеет прямолинейное очертание. Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют — реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.

Звездочка

Шестерня-звезда — это основная деталь цепной передачи, которая используется совместно с гибким элементом — цепью для передачи механической энергии.

Коронная шестерня

Коронная шестерня – это особый тип шестерен, их зубья находятся на боковой поверхности. Такая шестерня работает, как правило, в паре с прямозубой или с барабаном (цевочное колесо), состоящим из стержней. Такая передача используется в башенных часах.

Глава 8. зацепления зубчатые

Зацепления зубчатые относятся к передачам (подвиж­ным соединениям) и передают движение от двигателя к ис­полнитель­ным механизмам. К составным частям зубчатых передач отно­сятся зубчатые колеса (цилиндрические, кони­ческие), червяки, рейки.

Диаметр делительной ок­ружности d является од­ним из основных параметров, по кото­рому произ­водят расчет зубча­того ко­леса:

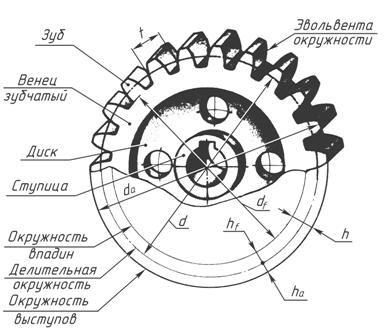
d = m × z ,

где z – число зубьев;

Модуль зацепления m – это часть диаметра делительной ок­ружности, приходящейся на один зуб:

где t – шаг зацепления.

Высота зуба :

где h _a – высота головки зуба, h _a = m ; h _f – высота ножки зуба, h _f = 1,25 m .

Диаметр окружности выступов зубьев :

d _a = d + 2 h _a = m ( z + 2).

Диаметр окружности впадин :

d _f = d – 2 h _f = m ( z – 2,5).

Служит для передачи вращения при параллельных осях валов.

ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.

Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …

Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …

Примечание. Ряд 1 следует предпочитать ряду 2 .

Служит для преобразования вращательного движения в возвратно-посту­пательное.

ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.

Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …

Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …

Примечание. Ряд 1 следует предпочитать ряду 2.

Служит для передачи вращательного движения между валами со скрещивающимися осями.

ГОСТ 19672-74 устанавливает два ряда значений модулей m (мм).

Ряд 1: … 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10 …

Ряд 2: … 1,5; 3; 3,5; 6; 7 …

Примечание. Ряд 1 следует предпочитать ряду 2.

Служит для передачи вращения при пересекающихся осях валов.

ГОСТ 9563-60 предусматривает два ряда модулей m  = 0,05…100 мм.

Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …

Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …

17. Конические зубчатые передачи с круговыми зубьями

Благодаря наклону и бочкообразной форме зубьев конические колеса с круго­вым зубом, более прочны, бесшумны и допускают большие отклонения при монтаже, чем прямозубые.

При конструировании конических колес с круговым зубом учитывают возможность нарезания их на станке.

В интервале 6—100 можно нарезать ко­лесо с любым числом зубьев в интервале 100—200 — только колеса с числом зубьев, которое можно разложить на множители.

Так, например, колесо с z = 107 не сле­дует конструировать, так как для его изго­товления придется делать специальное ко­лесо на делительную гитару станка.

Числа зубьев шестерен и колес ортогональной конической зубчатой передачи следует выбирать с учетом данных, приведенных в табл. 73.

Число зубьев цементованных ко­нических зубчатых колес рекомендуется определять по рис. 31.

Термически улучшенные конические зубчатые колеса могут выполняться с тем же или с увеличенным на 10—20 % числом зубьев.

Рис. 31. Номограмма для определения рекомендуе­мого числа зубьев конических шестерен (а = 20°; Σ = 90°):

Пример. Дано: d_e1 = 300мм, u = 4, β_n = 35°. По номограмме определяем z₁ = 25,5 ≈ 25.

73. Минимальные допустимые числа зубьев ортогональной конической передачи с круговыми зубьями при исходном контуре по ГОСТ 16202—81

Число зубьев

шестерни

Наименьшее число

зубьев колеса z₁

Число зубьев

шестерни

Наименьшее число

з убьев колеса z ₁

Модули. В качестве расчетного принят нормальный модуль m_nв середине ширины венца.

В качестве исходного для расчета вместо m_n может быть принят внешний окружной модуль m_te. Так, для редукторных передач с параметрами по ГОСТ 12289—76, в котором стандартизованы внешние делительные диаметры колес (d_e2), первоначально опре­деляют внешний окружной модуль m_te = d_e2 / z₂, который и принимают в качестве исходного для дальнейшего расчета.

При m_n < 2 исходным для расчета при­нимают только средний нормальный мо­дуль.

Модули m_n рекомендуется устанавливать по ГОСТ 9563—60, им соответствуют разво­ды резцов зуборезных головок по ГОСТ 11902—77 (табл. 74).

Угол наклона и направление линии зуба.

Расчетный угол наклона зуба β_n может на­ходиться в пределах 0—45°. Рекомендуется применять одно из значений ряда: 0; 10; 15; 20; 25; 30; 35; 40; 45°.

Предпочтителен к применению угол на­клона β_n = 35°. При z₁ от 6 до 17 рекомен­дуемые значения указаны в табл. 73.

Угол β_n целесообразно назначать таким, чтобы коэффициент осевого перекрытия ε_β был не менее 1,25;

при требовании максимальной плавно­сти работы передачи рекомендуется ε_β ≥ 1,6 (рис. 32).

При назначении угла β_n следует также учитывать, что с его увеличением возраста­ют нагрузки на опоры и валы.

В табл. 75 приведены формулы для оп­ределения величины и направления осевой и радиальной сил в зацеплении конических зубчатых колес с круговыми зубьями, а на рис. 33 — график для определения ве­личины и направления осевой силы в ор­тогональной конической передаче при угле профиля исходного контура a_n= 20°.

74. Разводы W₂ резцов зуборезных головок по ГОСТ 11902—77 и соответствующие им значения коэффициентов изменения расчетной толщины зуба шестерни х_τ1 при средних нормальных модулях m_n по ГОСТ 9563-60

Средний нормальный

модуль m_n, 1-й ряд

*δh_f — поправка на высоту ножки зуба вводится только при x_τ1 = 0 и двусторонней обра­ботке колеса.

ГОСТ 19326—73 предусматривает также 2-й ряд среднего нормального модуля m_n.

При совпадении направлений линий зу­ба с направлением вращения, если смот­реть со стороны вершины делительных ко­нусов ведущего конического зубчатого ко­леса понижающей передачи и ведомого конического зубчатого колеса повышающей передачи, осевые силы на них будут на­правлены от вершин делительных конусов.

Сопряженные зубчатые колеса имеют противоположные направления линий зуба.

При проектировании конических зубчатых колес с осевой формой зуба I в некоторых случаях расчетный угол наклона зубьев назначают с учетом номера резцов.

Рис. 32. График для определения коэффициента осевого перекрытия

Пример. Дано: b = 30мм, m_n = 4мм, β_n = 40°. По графику находят при b/m_n = 30/4 = 7,5; е_β = 1,54.

75. Формулы для определения сил в зацеплении

Силы

Ведущее зубчатое колесо

Ведомое зубчатое колесо

где T₁ и Т₂ — моменты на шестерне и колесе

1. Верхние знаки в формулах даны для случая, когда направление вращения рассматриваемого зубчатого колеса (если смотреть на него с вершины делительного кону­са) совпадает с направлением наклона зубьев, как показано на рис. 34; нижние знаки — при отсутствии такого совпадения.

2. Направление вращения по часовой стрелке — правое; против часовой стрелки — левое.

3. Направления действия сил F_x и F_r определяются по знакам (+ и -), указанным на рис. 34, получаемым в результате расчета по формулам.

Рис. 33. Осевые силы в зацеплении конических зубчатых колес с круговыми зубьями а_n = 20°, Σ = 90°

Зубчатое

колесо

Направление

наклона зубьев

Направление

вращения

шестерня: направление наклона — правое, направление вращения — правое;

колесо: левое, направление вращения — левое.

По номограмме определяем F_x1 = 0,79Fi; F_x2 = 0,19F_i, используемых при зубонарезании. Для этого предварительно определяют необходимый номер резцов по формуле

и округляют его до значений N по ГОСТ 11902—77. В приведенной формуле β’_n — предварительное значение угла накло­на зубa проектируемой передачи.

Рис. 34. Направления вращения и действия сил F_x и F_r

Зубчатое колесо

Направление наклона зубьев

Направление вращения

Далее окончательно устанавливают расчетный угол наклона зуба β_n по формуле

при исходном контуре по ГОСТ 16202—81.

Исходный контур. Под исходным конту­ром конических зубчатых колес с круговыми зубьями (рис. 35) подразумевают контур зубьев условной рейки, профиль которой и высотные размеры зубьев совпадают с од­ноименными элементами зубьев плоского исходного колеса в среднем нормальном сечении; шаг и толщину зубьев принимают соответственно равными окружному шагу и половине окружного шага плоского исход­ного колеса посередине ширины зубчатого венца, умноженным на косинус среднего угла наклона линии зубьев плоского исход­ного колеса; с = р_f= 0,25m_n.

В технически обоснованных случаях до­пускается неравенство делительных толщин зубьев s_n1 и s_n2 в паре исходных контуров, изменение глубины захода h_w, радиального зазора с и радиуса р_f(от 0,15m_n и до 0,35m_n) и соответственно граничной высоты h₁, а также применение переходной кривой, от­личной от дуги окружности, если указан­ные изменения не нарушают правильности зацепления и не препятствуют использова­нию стандартного инструмента.

Допускается применение профильной модификации исходного контура.

Конические передачи с круговыми зубьями (средний нормальный модуль m_n от 1мм и более) должны выполняться с параметрами и коэффициентами исходного контура по ГОСТ 16202—81:

угол главного профиля а_n = 20°;

коэффициент высоты головки h_a* = 1;

коэффициент высоты ножки h_f* = 1.25;

коэффициент граничной высоты h_t* = 2,08;

коэффициент радиуса кривизны пере­ходной кривой, являющейся дугой окруж­ности, р_f* = 0,25;

коэффициент глубины захода в паре ис­ходных контуров h_W* = 2;

коэффициент радиального зазора в паре исходных контуров с* = 0,25;

профиль в пределах граничной высоты — прямолинейный.

Примечание. При отсутствии до­полнительных указаний везде, где упоми­нается профиль зуба, имеется в виду про­филь в нормальном расчетном сечении.

Рис. 35. Исходный контур по ГОСТ 16202-81

Выбор осевой формы зубьев и номиналь­ного диаметра зуборезной головки.

1. В табл. 76 указаны диапазоны пара­метров конических зубчатых колес, опреде­ляющие возможные области использования осевых форм зубьев I, II и III, получивших наибольшее распространение. Осевая фор­ма зуба I показана на рис. 28, осевые фор­мы зуба II и III—на рис. 39 и 40.

При исходном контуре по ГОСТ 16202— 81 и расчетных углах наклона зуба β_n > 15º разграничение этих областей в зависимости от k = R/d и β_n устанавливается по рис. 36.

Зона, заштрихованная на графике пере­крещивающимися линиями, соответствует значениям k и β_n, при которых осевые формы зубьев I и II практически являются равноценными. Кривая линия, делящая рекомендуемую область применения зубчатых колес с осевой формой зуба III почти на две равные части, соответствует значениям k = 1/(2sinβ_n) при которых ис­ключается какое-либо сужение равновысоких зубьев, и они приобретают оптималь­ную форму.