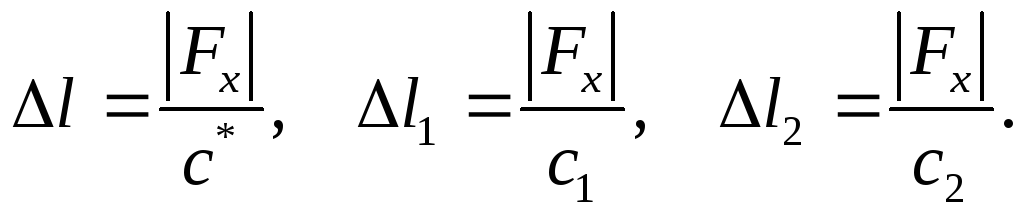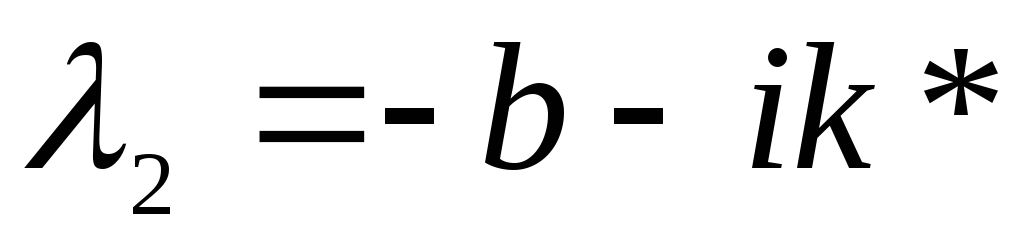Решение. При параллельном соединении пружин…

Как найти жесткость пружин соединенных последовательно?

¯F=kΔl(1), где в коэффициент пропорциональности называется жесткостью пружины (коэффициентом упругости) k. Жесткость (как свойство) — это характеристика упругих свойств тела, которое деформируют.

Какой формулой определяется коэффициент жесткости соединения из двух последовательно соединенных пружин?

Жесткость соединений пружин

При последовательном соединении N пружин жесткость соединения вычисляется при помощи формулы: 1k=1k1+1k2+⋯=N∑ i=11ki(2). Если пружины соединены параллельно, то результирующая жесткость равна: k=k1+k2+⋯+N∑i=1ki(3).

Какой формулой определяется коэффициент жесткости соединения из двух параллельных пружин?

Параллельное соединение системы пружин

В случае когда пружины соединены параллельно, величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так: k = k1 + k2 + … + ki.

Как рассчитать емкость конденсатора при последовательном соединении?

Общая емкость равнозначного (эквивалентного) конденсатора C = Q / U = Q / (U1 + U2 + U3), т. е. при последовательном соединении конденсаторов величина, обратная общей емкости, равна сумме обратных величин емкостей отдельных конденсаторов.

Как определить жесткость пружины по массе?

В итоге этих экспериментов появилась такая формула: kx=mg, где k – некий постоянный для данной пружины коэффициент, x – изменение длины пружины, m – ее масса, а g – ускорение свободного падения (примерное значение – 9,8 м/с²).

В чем обозначается жесткость пружины?

Обозначается буквой k, иногда D или c.

В чем измеряется жесткость?

В системе СИ коэффициент механической жёсткости измеряется в ньютонах на метр (Н/м).

Почему при параллельном соединении пружин?

Довольно часто встречается и параллельное соединение пружин. В этом случае смещение тела, которому передается сила, равна деформации каждой из них. . Построенная схема указывает на то, что жесткость пружин при параллельном соединении остается неизменной, но общий показатель возрастает в два раза.

Как рассчитать жесткость?

1. Измеряется длина пружины в вертикальном подвесе с одной свободной стороной изделия – L1;
2. Измеряется длина пружины с подвешенным грузом – L2. .
3. Вычисляется разница между последним и первым показателем длины – L;
4. Рассчитывается коэффициент упругости по формуле: k = F/L.

Чем отличается последовательное соединение от параллельного?

При последовательном соединении проводников сила тока во всех проводниках одинакова. При этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников. При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов.

Что происходит при последовательном соединении конденсаторов?

При последовательном соединении конденсаторов уменьшается общая емкость и увеличивается общее напряжение конденсаторов. А общее напряжение будет равняться сумме напряжений всех конденсаторов. Например: мы имеем три конденсатора по 30 мкФ x 100 В каждый.

Чему равны IUR при последовательном соединении проводников?

Проводники в электрических цепях могут соединяться последовательно и параллельно. При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова: I1 = I2 = I.

Что называется последовательным соединением конденсаторов?

Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).

Как найти емкость конденсатора по схеме?

По формуле С = t/3R, где t – время падения напряжения, вычисляем ёмкость конденсатора в фарадах, если единицы измерения сопротивление резистора выразили в омах, а время в секундах.

Как рассчитывается электрическая емкость конденсатора?

Его значение вычисляется по формуле: E=14πεε0qr2 E = 1 4 π ε ε 0 q r 2 , где q обозначают заряд внутренней сферы, r=R1+x r = R 1 + x — расстояние от центра сферы. Нахождение заряда предполагает применение определения емкости конденсатора С: q=CU q = C U .

Параллельное соединение пружин

При параллельном соединении двух пружин, имеющих коэффициенты жесткости с₁, с₂ (рис. 2.5), смещение тела равно деформации каждой из пружин:

. (2.9)

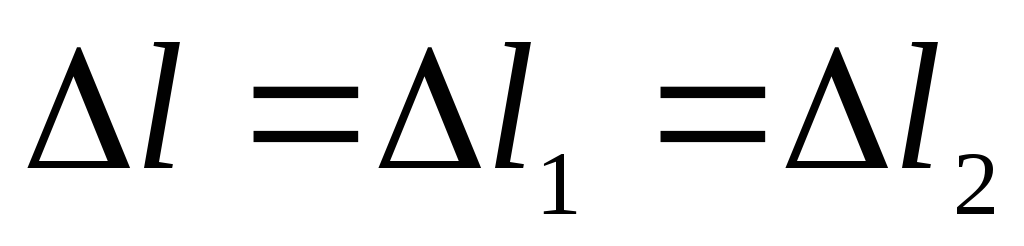
Рис. 2.5 Параллельное соединение пружин

Сила упругости эквивалентной пружины с коэффициентом жесткости с* будет равна сумме сил упругости двух установленных пружин, откуда с учетом (2.9) получаем

,

. (2.10)

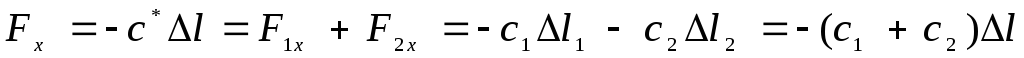
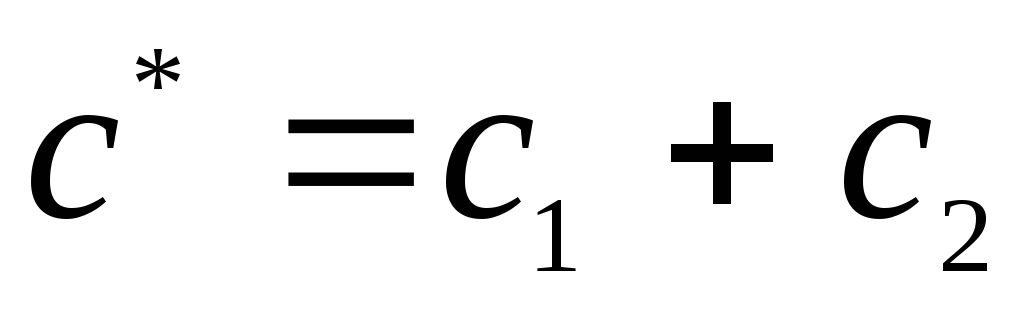
Последовательное соединение пружин

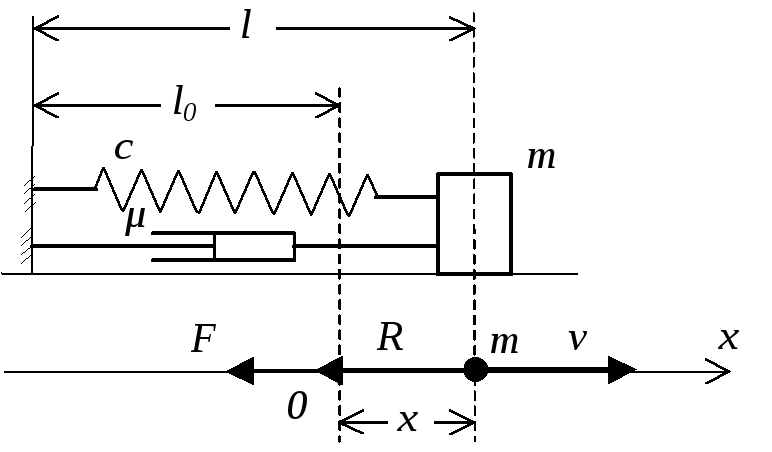
При последовательном соединении двух пружин, имеющих коэффициенты жесткости с₁, с₂ (рис. 2.6), смещение тела равно сумме деформаций пружин:

. (2.11)

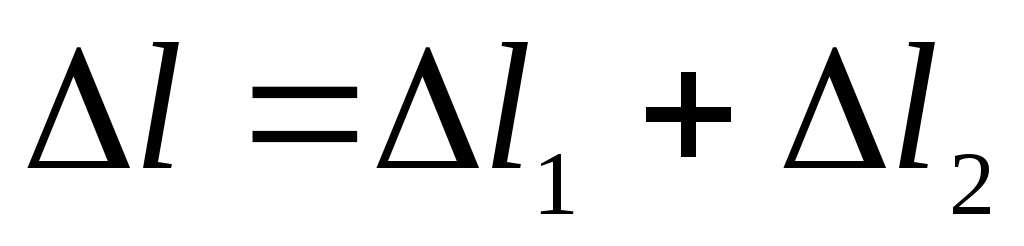
Рис. 3.6 Последовательное соединение пружин

Сила упругости эквивалентной пружины с коэффициентом жесткости с* будет равна каждой из сил упругости установленных пружин, откуда

,

,

Окончательно с учетом (2.11) получаем

. (2.12)

Влияние сопротивления на свободные колебания

Пусть на точку массы m, совершающую прямолинейное движение, действуют две силы (рис. 2.7):

Восстанавливающая сила (сила упругости пружины): .

Сила сопротивления, пропорциональная скорости движения точки (сила сопротивления демпфера): .

Рис. 2.7 Движение массы с демпфированием

Дифференциальное уравнение движения точки запишется как

;

,

, , (2.13)

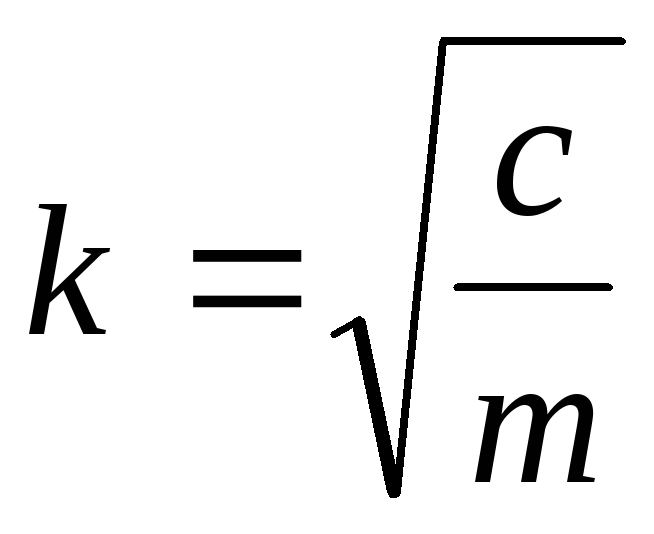
получаем линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами:

. (2.14)

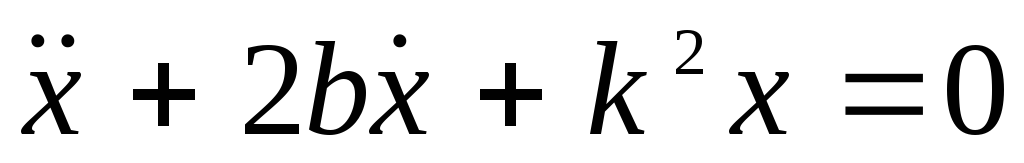
Характеристическое уравнение имеет вид

, (2.15)

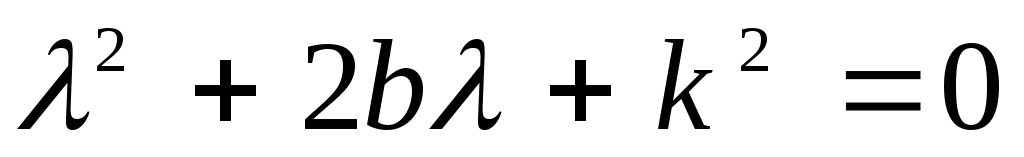
его корни равны

, (2.16)

где – дискриминант.

Как известно из курса высшей математики, общее решение дифференциального уравнения (2.14) существенно зависит от знака дискриминанта , т.е. от соотношения между b и k.

1-й случай (малое сопротивление): b  k , D  0.

Обозначим 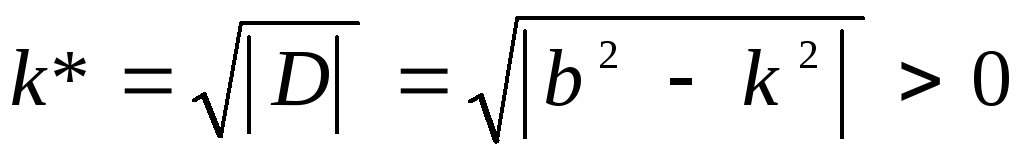, причем k*  k. Тогда корни (2.16) характеристического уравнения будут комплексно сопряженными:

,

Общее решение дифференциального уравнения (2.14) в данном случае имеет вид

, (2.17)

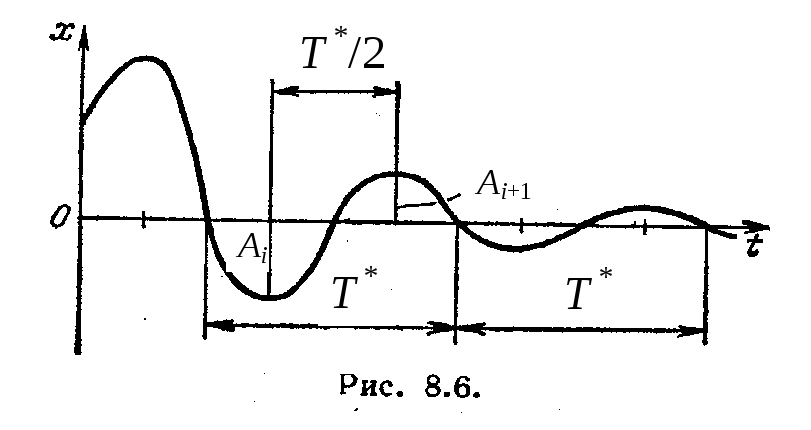
это затухающие колебания с частотой k * и периодом 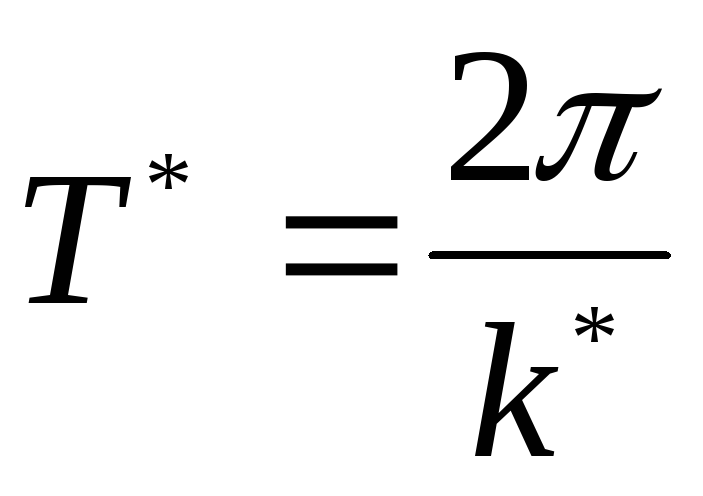(рис.3.8).

Амплитуда колебаний убывает со временем. Отношение последующей амплитуды к предыдущей называется декрементом затухания:

< 1 (2.18)

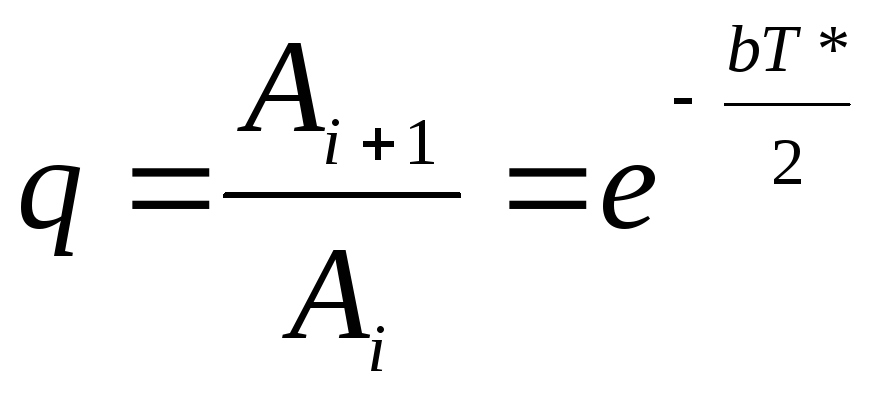
Рис. 2.8 Затухающие колебания

Часто используется также логарифмический декремент .

Таким образом, амплитуды образуют геометрическую прогрессию с показателем q, меньшим единицы.

Видим также, что наличие сопротивления приводит к уменьшению частоты колебаний (k *  k) и к увеличению их периода (Т * > Т).

2-й случай (граничный): b = k , D = 0.

Корни (2.16) характеристического уравнения получаются кратные, 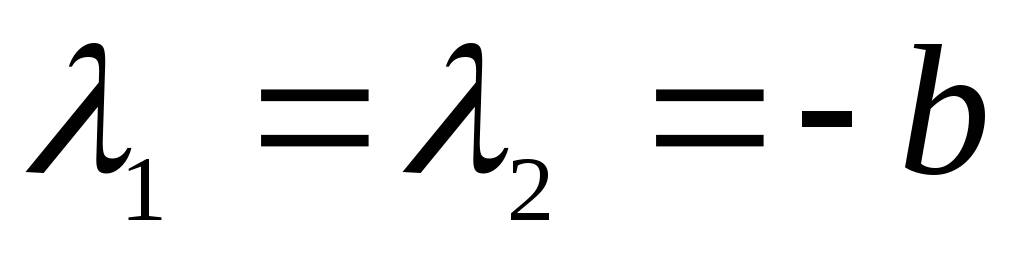, и решение дифференциального уравнения (2.14) приобретает вид

. (2.19)

Поскольку экспонента убывает быстрее, чем растёт линейная функция времени, в зависимости от начальных условий движения получим ту или иную картину затухающего апериодического (т.е. не колебательного) движения (рис.2.9).

3-й случай (большое сопротивление): b > k, D > 0.

В этом случае обозначим >0, и оба корня (2.16) характеристического уравнения будут действительными и отрицательными:

< 0, < 0,

. (2.20)

Рис. 2.9 График затухающего апериодического движения

Здесь также получаем затухающие апериодическое движение, графики будут такие же, как и в случае b= k.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Силы упругости

Как вы уже знаете из курса физики основной школы, силы упругости связаны с деформацией тел, то есть изменением их формы и (или) размеров.

Связанная с силами упругости деформация тел не всегда заметна (подробнее мы остановимся на этом ниже). По этой причине свойства сил упругости изучают обычно, используя для наглядности пружины: их деформация хорошо видна на глаз.

Подвесим к пружине груз (рис. 15.1, а). (Будем считать, что массой пружины можно пренебречь.) Пружина растянется, то есть деформируется.

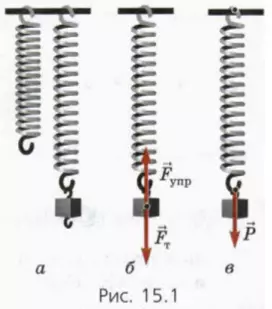
На подвешенный груз действуют сила тяжести _т и приложенная со стороны растянутой пружины сила упругости _упр (рис. 15.1, б). Она вызвана деформацией пружины.

Согласно третьему закону Ньютона на пружину со стороны груза действует такая же по модулю, но противоположно направленная сила (рис. 15.1, в). Эта сила – вес груза: ведь это сила, с которой тело растягивает вертикальный поднес (пружину).

Силы _упр и , с которыми груз и пружина взаимодействуют друг с другом, связаны третьим законом Ньютона и поэтому имеют одинаковую физическую природу. Следовательно, вес – это тоже сила упругости. (Действующая на пружину со стороны груза сила упругости (вес груза) обусловлена деформацией груза. Эта деформация незаметна, если грузом является гиря или брусок. Чтобы деформация груза стала тоже заметной, можно в качестве груза взять массивную пружину: мы увидим, что она растянется.) Действуя на пружину, вес груза растягивает ее, то есть является причиной ее деформации. (Во избежание недоразумений подчеркнем еще раз, что пружину, к которой подвешен груз, растягивает не приложенная к грузу сила тяжести груза, а приложенная к пружине со стороны груза сила упругости (вес груза).)

На этом примере мы видим, что силы упругости являются и следствием, и причиной упругой деформации тел:
– если тело деформировано, то со стороны этого тела действуют силы упругости (например, сила _упр на рисунке 15.1, б);
– если к телу приложены силы упругости (например, сила на рисунке 15.1, в), то это тело деформируется.

? 1. Какие из изображенных на рисунке 15.1 сил
а) уравновешивают друг друга, если груз покоится?
б) имеют одинаковую физическую природу?
в) связаны третьим законом Ньютона?
г) перестанут быть равными по модулю, если груз будет двигаться с ускорением, направленным вверх или вниз?

Всегда ли деформация тела заметна? Как мы уже говорили, «коварная» особенность сил упругости состоит в том, что связанная с ними деформация тел далеко не всегда заметна.

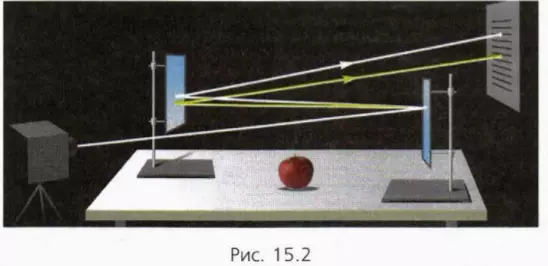
Деформация стола, обусловленная весом лежащего на нем яблока, незаметна на глаз (рис. 15.2).

И тем не менее она есть: только благодаря силе упругости, возникшей вследствие деформации стола, он удерживает яблоко! Деформацию стола можно обнаружить с помощью остроумного опыта. На рисунке 15.2 белые линии схематически обозначают ход луча света, когда яблока на столе нет, а желтые линии – ход луча света, когда яблоко лежит на столе.

? 2. Рассмотрите рисунок 15.2 и объясните, благодаря чему деформацию стола удалось сделать заметной.

Некоторая опасность состоит в том, что, не заметив деформации, можно не заметить и связанной с ней силы упругости!

Так, в условиях некоторых задач фигурирует «нерастяжимая нить». Под этими словами подразумевают, что можно пренебречь только величиной деформации нити (увеличением ее длины), но нельзя пренебрегать силами упругости, приложенными к нити или действующими со стороны нити. На самом деле «абсолютно нерастяжимых нитей» нет: точные измерения показывают, что любая нить хоть немного, но растягивается.

Например, если в описанном выше опыте с грузом, подвешенным к пружине (см. рис. 15.1), заменить пружину «нерастяжимой нитью», то под весом груза нить растянется, хотя ее деформация и будет незаметной. А следовательно, будут присутствовать и все рассмотренные силы упругости. Роль силы упругости пружины будет играть сила натяжения нити, направленная вдоль нити.

? 3. Сделайте чертежи, соответствующие рисунку 15.1 (а, б, в), заменив пружину нерастяжимой нитью. Обозначьте на чертежах силы, действующие на нить и на груз.

? 4. Два человека тянут в противоположные стороны веревку с силой 100 Н каждый.
а) Чему равна сила натяжения веревки?
б) Изменится ли сила натяжения веревки, если один ее конец привязать к дереву, а за другой конец тянуть с силой 100 Н?

Природа сил упругости

Силы упругости обусловлены силами взаимодействия частиц, из которых состоит тело (молекул или атомов). Когда тело деформируют (изменяют его размеры или форму), расстояния между частицами изменяются. Вследствие этого между частицами возникают силы, стремящиеся вернуть тело в недеформированное состояние. Это и есть силы упругости.

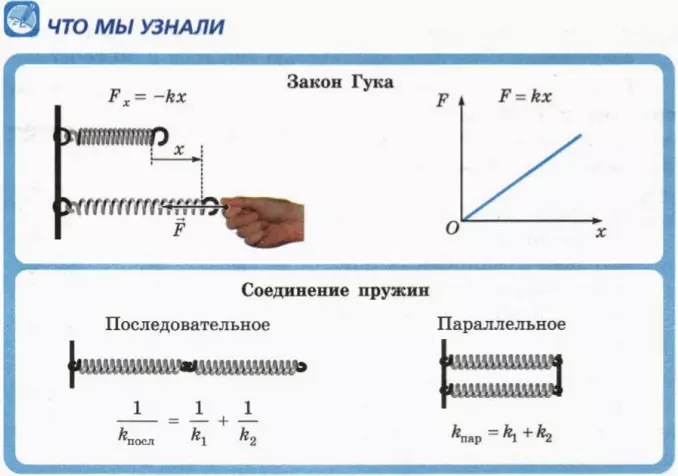
2. Закон Гука

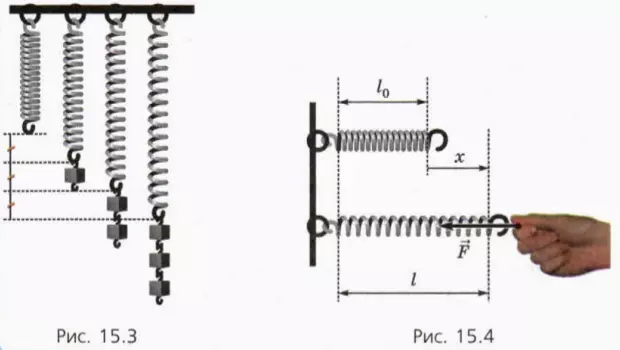
Будем подвешивать к пружине одинаковые гирьки. Мы заметим, что удлинение пружины пропорционально числу гирек (рис. 15.3).

Это означает, что деформация пружины прямо пропорциональна силе упругости.

Обозначим деформацию (удлинение) пружины

где l – длина деформированной пружины, а l – длина недеформированной пружины (рис. 15.4). Когда пружина растянута, x > 0, а проекция действующей со стороны пружины силы упругости F_x < 0. Следовательно,

Знак «минус» в этой формуле напоминает, что приложенная со стороны деформированного тела сила упругости направлена противоположно деформации этого тела: растянутая пружина стремится сжаться, а сжатая – растянуться.

Коэффициент k называют жесткостью пружины. Жесткость зависит от материала пружины, ее размеров и формы. Единица жесткости 1 Н/м.

Соотношение (2) называют законом Гука в честь английского физика Роберта Гука, открывшего эту закономерность. Закон Гука справедлив при не слишком большой деформации (величина допустимой деформации зависит от материала, из которого изготовлено тело).

Формула (2) показывает, что модуль силы упругости F связан с модулем деформации x соотношением

Из этой формулы следует, что график зависимости F(x) – отрезок прямой, проходящий через начало координат.

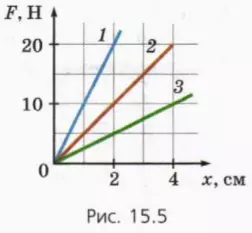
? 5. На рисунке 15.5 приведены графики зависимости модуля силы упругости от модуля деформации для трех пружин.
а) У какой пружины наибольшая жесткость?
б) Чему равна жесткость самой мягкой пружины?

? 6. Груз какой массы надо подвесить к пружине жесткостью 500 Н/м, чтобы удлинение пружины стало равным 3 см?

Важно отличать удлинение пружины x от ее длины l. Различие между ними показывает формула (1).

? 7. Когда к пружине подвешен груз массой 2 кг, ее длина равна 14 см, а когда подвешен груз массой 4 кг, длина пружины равна 16 см.
а) Чему равна жесткость пружины?
б) Чему равна длина недеформированной пружины?

3. Соединение пружин

Последовательное соединение

Возьмем одну пружину жесткостью k (рис, 15.6, а). Если растягивать ее силой (рис. 15.6, б), ее удлинение выражается формулой

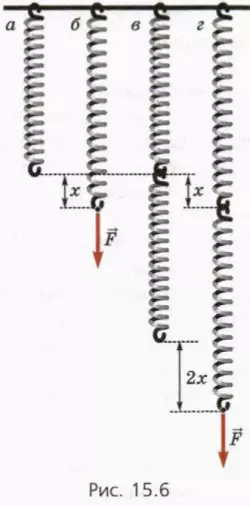
Возьмем теперь вторую такую же пружину и соединим пружины, как показано на рисунке 15.6, в. В таком случае говорят, что пружины соединены последовательно.

Найдем жесткость k_посл системы из двух последовательно соединенных пружин.

Если растягивать систему пружин силой , то сила упругости каждой пружины будет равна по модулю F. Общее же удлинение системы пружин будет равно 2x, потому что каждая пружина удлинится на x (рис. 15.6, г).

где k – жесткость одной пружины.

Итак, жесткость системы из двух одинаковых последовательно соединенных пружин в 2 раза меньше, чем жесткость каждой из них.

Если последовательно соединить пружины с разной жесткостью, то силы упругости пружин будут одинаковы. А общее удлинение системы пружин равно сумме удлинений пружин, каждое из которых можно рассчитать с помощью закона Гука.

? 8. Докажите, что при последовательном соединении двух пружин
1/k_посл = 1/k₁ + 1/k₂, (4)
где k₁ и k₂ – жесткости пружин.

? 9. Чему равна жесткость системы двух последовательно соединенных пружин жесткостью 200 Н/м и 50 Н/м?

В этом примере жесткость системы двух последовательно соединенных пружин оказалась меньше, чем жесткость каждой пружины. Всегда ли это так?

? 10. Докажите, что жесткость системы двух последовательно соединенных пружин меньше жесткости любой из пружин, образующих систему.

Параллельное соединение

На рисунке 15.7 слева изображены параллельно соединенные одинаковые пружины.

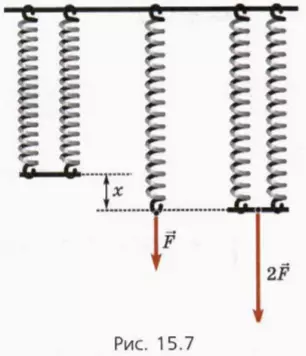
Обозначим жесткость одной пружины k, а жесткость системы пружин k_пар.

? 11. Докажите, что k_пар = 2k.

Подсказка. См. рисунок 15.7.

Итак, жесткость системы из двух одинаковых параллельно соединенных пружин в 2 раза больше жесткости каждой из них.

? 12. Докажите, что при параллельном соединении двух пружин жесткостью k₁ и k₂

Подсказка. При параллельном соединении пружин их удлинение одинаково, а сила упругости, действующая со стороны системы пружин, равна сумме их сил упругости.

? 13. Две пружины жесткостью 200 Н/м и 50 Н/м соединены параллельно. Чему равна жесткость системы двух пружин?

? 14. Докажите, что жесткость системы двух параллельно соединенных пружин больше жесткости любой из пружин, образующих систему.

Дополнительные вопросы и задания

15. Постройте график зависимости модуля силы упругости от удлинения для пружины жесткостью 200 Н/м.

16. Тележку массой 500 г тянут по столу с помощью пружины жесткостью 300 Н/м, прикладывая силу горизонтально. Трением между колесами тележки и столом можно пренебречь. Чему равно удлинение пружины, если тележка движется с ускорением 3 м/с 2 ?

17. К пружине жесткостью k подвешен груз массой m. Чему равно удлинение пружины, когда груз покоится?

18. Пружину жесткостью k разрезали пополам. Какова жесткость каждой из образовавшихся пружин?

19. Пружину жесткостью k разрезали на три равные части и соединили их параллельно. Какова жесткость образовавшейся системы пружин?

20. Докажите, что жесткость и последовательно соединенных одинаковых пружин в n раз меньше жесткости одной пружины.

21. Докажите, что жесткость n параллельно соединенных одинаковых пружин в n раз больше жесткости одной пружины.

22. Если две пружины соединить параллельно, то жесткость системы пружин равна 500 Н/м, а если эти же пружины соединить последовательно, то жесткость системы пружин равна 120 Н/м. Чему равна жесткость каждой пружины?

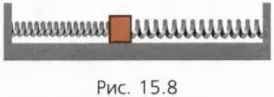
23. Находящийся на гладком столе брусок прикреплен к вертикальным упорам пружинами жесткостью 100 Н/м и 400 Н/м (рис. 15.8). В начальном состоянии пружины не деформированы. Чему будет равна действующая на брусок сила упругости, если его сдвинуть на 2 см вправо? на 3 см влево?

Последовательное соединение пружин

Пружины являются важным элементом самых различных механизмов. Для изменения основных эксплуатационных свойств проводится использование нескольких подобных изделий, которые соединяются различным образом. Тип применяемого метода соединения учитывается при проведении самых различных расчетов.

Основные методы крепления пружин

При проведении расчетов уделяется внимание тому, каким образом проводится соединение пружин. Этот момент оказывает влияние на следующее:

1. Жесткость системы. Этот показатель встречается практически во всех проводимых расчетах при последовательном подключении деталей. Зависит он от самых различных моментов, к примеру, коэффициента жесткости каждого.
2. Требуемое усилие для сжатия или растяжения. Рассматриваемая деталь применяется часто по причине того, что может обеспечивает накопление кинетической энергии.
3. Размер кинетической и потенциальной энергии. После того как изделие было выведено из положения равновесия начинает накапливаться кинетическая энергия. При этом она сохраняется на протяжении всего периода, пока к телу приложено усилие.
4. Вероятность возникновения свободного колебательного движения, а также степень сопротивления подобному явлению. Для расчетов колебательного движения также применяются специальные формулы.

Бывают самые различные способы соединения пружин, но наибольшее распространение получил метод последовательного и параллельного подключения.

Они характеризуются довольно большим количеством особенностей. Прежде чем рассматривать применение подобных способов соединения следует уделить внимание особенностям самого изделия:

1. Деталь изготавливается из проволоки, которая получается методом проката. Она обладает высоким показателем упругости, а также устойчивостью к воздействию окружающей среды.
2. Прокат изготавливают из специального сплава, способного выдерживать периодическую деформацию. Под заказ может производится деталь из обычных углеродистых сплавов или легированных металлов, все зависит от конкретного случая.
3. Проволока накручивается в виде колец по спирали. При этом должна выдерживаться едина ось, которая определяет распространение силы в одном направлении.
4. Выделяют два основных типа детали: растяжения и сжатия. Первый вариант исполнения характеризуется тем, что витки находятся практически вплотную. В случае изготовления изделия для сжатия выдерживается определенный зазор, который позволяет кольцам сближаться, а самому изделию сжиматься.
5. Характеризуется изделие самыми различными показателями. Примером можно назвать диаметр проволоки, созданных колец из нее, шаг расположения витков. Все эти параметры указываются в технической документации.

Сегодня они встречаются практически повсеместно. Это связано с тем, что подобное изделие практически незаменимо в случае, когда требуется возвратно-поступательное движение.

Последовательное соединение

При создании многих механизмов применяется последовательное соединение пружин. Среди особенностей этого метода отметим нижеприведенные моменты:

1. Наиболее важным параметром можно назвать коэффициент жесткости. Он определяет практически все свойства детали. Коэффициент жесткости при последовательном соединении пружин равен каждому из показателей упругости.
2. Также не стоит забывать о том, что показатель смещения тела равен сумме деформации витков. Любой тип рассматриваемого изделия характеризуется максимальным удлинение и сжатием. В случае максимального сжатия кольца расположены вплотную, зазор отсутствует практически полностью. При растяжении есть вероятность деформации витков, из-за чего изделие попросту потеряет свои основные характеристики.

Для расчетов могут применяться самые различные формулы. Среди особенностей этого метода соединения пружин отметим следующее:

1. Для начала берется одна деталь с жесткостью K, сила растяжения выражается следующей формулой: x=F/k.
2. Следующий шаг заключается в подсоединении второй детали. Для этого могут применяться различные крепежные элементы. При этом две пружины разной длины будут находится в одной системе.
3. Если приложить усилие для растягивания обоих изделий, то сила упругости каждой будет равна по модулю. При этом удлинение каждой будет равно х.

Приведенная выше информация указывает на то, что упругость системы двух последовательно соединенных изделий будет примерно в два раза меньше. При этом удлинение будет равно сумме удлинения каждой в отдельности.

Применяемый метод соединения получил весьма широкое распространение. Однако, в некоторых случаях целесообразно применять параллельный метод соединения.

Параллельное соединение

Довольно часто встречается и параллельное соединение пружин. В этом случае смещение тела, которому передается сила, равна деформации каждой из них. Зачастую параллельно соединенные пружины используются тогда, когда нужно передать большее усилие. Особенностями этого метода назовем следующее:

1. В рассматриваемом случае жесткости пружины обозначаются буквой k. Построенная схема указывает на то, что жесткость пружин при параллельном соединении остается неизменной, но общий показатель возрастает в два раза.
2. Показатель удлинения остается неизменным. При этом сила упругости возрастает в два раза в случае, если обе детали обладают схожими эксплуатационными характеристиками.

Проблемой применения подобной системы можно назвать то, что обе детали должны обладать одинаковой длиной в состоянии покоя. В противном случае сила упругости будет распределяться неравномерно, при этом есть вероятность критической деформации одной из них.

Влияние сопротивления на свободные колебания

Особенности детали определяют то, что при ее применении есть вероятность возникновения свободного колебательного движения. При этом имеет значение, какими особенностями обладает параллельно и последовательно соединенные пружины. Среди особенностей влияния сопротивления на свободное колебание отметим следующие моменты:

1. Проведенные тесты указывают на то, что параллельно соединенные пружины препятствуют возникновению свободного колебания. Это можно связать с существенным увеличением жесткости всей системы.
2. При последовательном расположении есть вероятность снижения сопротивления, так как расстояние между точкой крепления и телом существенно увеличивается.

Именно поэтому для существенного снижения колебательного вращения на момент эксплуатации системы рекомендуется использовать параллельный метод подключения.

Динамика несвободного движения

Еще одним важным показателем можно назвать динамику несвободного движения. Она может варьировать в достаточно большом диапазоне.

Распространенные последовательно соединенные пружины могут обеспечивать условия для несвободного движения тела. Динамика может нарастать в зависимости от длины в свободном состоянии и передаваемого усилия.

Как определить жесткость системы при последовательном соединении пружин?

Довольно большое количество проблем возникает на момент вычисления жесткости системы при последовательном соединении. Особенностями проводимого расчета в этом случае назовем следующее:

1. Важным показателем можно назвать жесткость, которая варьирует в достаточно большом диапазоне. Она во многом определяет свойства изделия. При слишком большой жесткости приходится прикладывать большее усилие для растяжения или сжатия детали.
2. Телу придается определенное усилие (F), которое становится причиной удлинения тела на величину x.
3. Для расчета применяется формула: k=F/(2x)=1/2F/x=k/2.

Приведенная выше информация указывает на то, что жесткость всей системы в этом случае в два раза меньше показателя жесткости каждого изделия. При этом формула применима только в том случае, если применяемые варианты исполнения для соединения обладают одинаковыми эксплуатационными характеристиками.

Определить жесткость системы пружин можно при самостоятельном проведении соответствующих расчетов. Сегодня система двух пружин получила весьма широкое распространение, так как при ее применении можно добиться требующихся результатов. Однако, прежде чем ее использовать следует провести соответствующие расчеты.