Гармонические колебания пружинного маятника
Один конец пружины закреплен, к другому концу прикреплено тело $m$ рис.1.
Рисунок 1. Пружинный маятник. Автор24 — интернет-биржа студенческих работ
Длина пружины без деформации равна $l_0$. При растяжении или сжатии этой пружины до длины $l$ возникает сила упругости ($vec F$), которая хочет вернуть пружине первоначальную длину. Если изменения длины пружины мало и равно:
то выполняется закон Гука, в соответствии с которым сила упругости прямо пропорциональна изменению длины пружины:
где $k$ — коэффициент упругости пружины.
Уравнение колебаний пружинного маятника
В таком случае уравнение движения тела, которое присоединено к концу пружины можно записать так:
$momega^2=k$, тогда дифференциальное уравнение (3) можно переписать в виде:
$y=y_mcos (omega t+delta) (5),$
где $y_m$ — амплитуда колебаний (максимальное смещение груза от положения равновесия), является решением уравнения (4) при любых постоянных значениях $y_m$ и $delta$.
Частота и период колебаний пружинного маятника
Груз на пружине выполняет гармонические колебания:
круговая (циклическая) частота которых равна:
период колебаний составляет:
частота колебаний его:
Мы видим в (7), что период колебаний пружинного маятника не зависит от амплитуды. Данное свойство колебаний называют изохронностью. Колебания пружинного маятника являются изохронными, пока выполняется закон Гука. Если растяжения становятся большими, то закон Гука будет нарушаться, тогда возникает зависимость периода колебаний от амплитуды.
Готовые работы на аналогичную тему
Амплитуда и начальная фаза колебаний пружинного маятника
Амплитуду колебаний ($y_m$) и начальную фазу ($delta$) невозможно определить из дифференциального уравнения (4). Данные неизменные параметры колебаний определяют исходя из начальных условий колебаний. Например, задают:
- смещение $y$ в момент времени принимаемы за $t=0$;
- и начальную скорость ($dot
$) в этот же момент времени.
Дифференциальное уравнение (4) справедливо при любых начальных условиях. Поскольку это уравнение может описывать любые колебания, которые способна совершать наша колебательная система. Конкретное колебание выделяют из этого комплекса при определении постоянных $y_m$ и $delta$.
Энергия колебаний пружинного маятника
Потенциальная энергия тела, подвешенного на пружине, задается выражением:
Принимая во внимание гармонический закон изменения $y$ (5), получим, что потенциальная энергия изменяется во времени:
$U(t)=frac
Кинетическую энергию определяют как:
Скорость движения тела на пружине вдоль оси $Y$ найдем как первую производную от $y(t)$ по времени:
$v=v_y=dot
Закон изменения кинетической энергии в зависимости от времени с учетом (12) запишем как:
$E_k=m y_m^2omega^2sin^2 (omega t+delta) (13),$
где учитывая формулу (6), окончательно получим:
$E_k=k y_m^2sin^2 (omega t+delta)=frac<1><4>k y_m^2(1-cos 2(omega t+delta)) (14).$
Формулы (10) и (14) показывают, что кинетическая и потенциальная энергии колеблющегося пружинного маятника изменяются во времени. Они сами выполняют гармонические колебания около средней величины, равной $frac<1> <4>k y_m^2$ с удвоенной циклической частотой $2omega$.
В тот момент времени, когда кинетическая энергия максимальна, потенциальная энергия равна нулю и наоборот. При этом полная механическая энергия, равная сумме кинетической и потенциальной энергии не изменяется:
При этом полная энергия колебаний пружинного маятника, если учесть выражения (10) и (14), равна:
Выражение (5) является решением дифференциального уравнения (15), если круговая частота колебаний определятся при помощи выражения (6), амплитуда – формулой (16). Так, если задана полная механическая энергия $E$, то амплитуда колебаний ($y_m$) не является произвольной величиной. При этом произвол имеется только в определении начальной фазы колебаний $delta$, которую определяют начальные условия. Чтобы определить $delta$ достаточно одного начального условия:
- либо нужно иметь начальное смещение;
- либо начальную скорость.
Наличие в решении единственной произвольной константы связывают с тем, что уравнение (15) является дифференциальным уравнением первого порядка по времени.
Заметим, что энергию в уравнении (15) можно рассматривать как параметр, принимающий любые значения большие нуля, которые определяют начальные условия колебаний. В этом случае уравнение (15) считают эквивалентным уравнению (4).
На основе закона сохранения энергии (15) сделаем следующие выводы:
Наибольшая кинетическая энергия пружинного маятника равна его наибольшей энергии потенциальной энергии.
Данный вывод очевиден, так как потенциальная энергия маячтника максимальна при смещении точки выполняющей колебания на максимально возможное расстояние, при этом скорость, а соответственно и кинетическая энергия осциллятора равна нулю.
Наибольшую кинетическую энергию колебательная система имеет тогда, когда она проходит положение равновесия ($x=0$), то есть потенциальная энергия равна нулю.
где $V$ — максимальная скорость.
Средняя кинетическая энергия пружинного маятника ($E_
Потенциальная и кинетическая энергия. Закон сохранения механической энергии
1. Камень, упав с некоторой высоты на Землю, оставляет на поверхности Земли вмятину. Во время падения он совершает работу по преодолению сопротивления воздуха, а после касания земли — работу по преодолению силы сопротивления почвы, поскольку обладает энергией. Если накачивать в закрытую пробкой банку воздух, то при некотором давлении воздуха пробка вылетит из банки, при этом воздух совершит работу по преодолению трения пробки о горло банки, благодаря тому, что воздух обладает энергией. Таким образом, тело может совершить работу, если оно обладает энергией. Энергию обозначают буквой ( E ) . Единица работы — ( [E,] ) = 1 Дж.
При совершении работы изменяется состояние тела и изменяется его энергия. Изменение энергии равно совершенной работе: ( E=A ) .
2. Потенциальной энергией называют энергию взаимодействия тел или частей тела, зависящую от их взаимного положения.
Поскольку тела взаимодействуют с Землёй, то они обладают потенциальной энергия взаимодействия с Землёй.
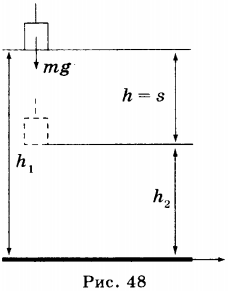
Если тело массой ( m ) падает с высоты ( h_1 ) до высоты ( h_2 ) , то работа силы тяжести ( F_т ) на участке ( h=h_1-h_2 ) равна: ( A = F_тh = mgh = mg(h_1 — h_2) ) или ( A = mgh_1 — mgh_2 ) (рис. 48).
В полученной формуле ( mgh_1 ) характеризует начальное положение (состояние) тела, ( mgh_2 ) характеризует конечное положение (состояние) тела. Величина ( mgh_1=E_ <п1>) — потенциальная энергия тела в начальном состоянии; величина ( mgh_2=E_ <п2>) — потенциальная энергия тела в конечном состоянии.
Можно записать ( A=E_<п1>-E_ <п2>) , или ( A=-(E_<п2>-E_<п1>) ) , или ( A=-E_ <п>) .
Таким образом, работа силы тяжести равна изменению потенциальной энергии тела. Знак «–» означает, что при движении тела вниз и соответственно при совершении силой тяжести положительной работы потенциальная энергия тела уменьшается. Если тело поднимается вверх, то работа силы тяжести отрицательна, а потенциальная энергия тела увеличивается.
Если тело находится на некоторой высоте ( h ) относительно поверхности Земли, то его потенциальная энергия в данном состоянии равна ( E_п=mgh ) . Значение потенциальной энергии зависит от того, относительно какого уровня она отсчитывается. Уровень, на котором потенциальная энергия равна нулю, называют нулевым уровнем.
В отличие от кинетической энергии потенциальной энергией обладают покоящиеся тела. Поскольку потенциальная энергия — это энергия взаимодействия, то она относится не к одному телу, а к системе взаимодействующих тел. В данном случае эту систему составляют Земля и поднятое над ней тело.
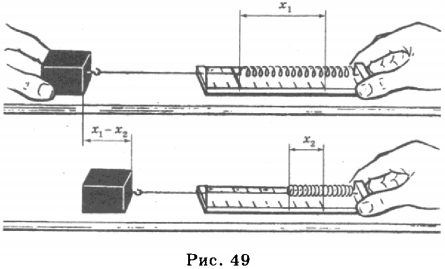
3. Потенциальной энергией обладают упруго деформированные тела. Предположим, что левый конец пружины закреплён, а к правому её концу прикреплён груз. Если пружину сжать, сместив правый её конец на ( x_1 ) , то в пружине возникнет сила упругости ( F_ <упр1>) , направленная вправо (рис. 49).
Если теперь предоставить пружину самой себе, то её правый конец переместится, удлинение пружины будет равно ( x_2 ) , а сила упругости ( F_ <упр2>) .
Работа силы упругости равна
( kx_1^2/2=E_ <п1>) — потенциальная энергия пружины в начальном состоянии, ( kx_2^2/2=E_ <п2>) — потенциальная энергия пружины во конечном состоянии. Работа силы упругости равна изменению потенциальной энергии пружины.
Можно записать ( A=E_<п1>-E_ <п2>) , или ( A=-(E_<п2>-E_<п1>) ) , или ( A=-E_ <п>) .
Знак «–» показывает, что при растяжении и сжатии пружины сила упругости совершает отрицательную работу, потенциальная энергия пружины увеличивается, а при движении пружины к положению равновесия сила упругости совершает положительную работа, а потенциальная энергия уменьшается.
Если пружина деформирована и её витки смещены относительно положения равновесия на расстояние ( x ) , то потенциальная энергия пружины в данном состоянии равна ( E_п=kx^2/2 ) .
4. Движущиеся тела так же могут совершить работу. Например, движущийся поршень сжимает находящийся в цилиндре газ, движущийся снаряд пробивает мишень и т.п. Следовательно, движущиеся тела обладают энергией. Энергия, которой обладает движущееся тело, называется кинетической энергией. Кинетическая энергия ( E_к ) зависит от массы тела и его скорости ( E_к=mv^2/2 ) . Это следует из преобразования формулы работы.
Работа ( A=FS ) . Сила ( F=ma ) . Подставив это выражение в формулу работы, получим ( A=maS ) . Так как ( 2aS=v^2_2-v^2_1 ) , то ( A=m(v^2_2-v^2_1)/2 ) или ( A=mv^2_2/2-mv^2_1/2 ) , где ( mv^2_1/2=E_ <к1>) — кинетическая энергия тела в первом состоянии, ( mv^2_2/2=E_ <к2>) — кинетическая энергия тела во втором состоянии. Таким образом, работа силы равна изменению кинетической энергии тела: ( A=E_<к2>-E_ <к1>) , или ( A=E_к ) . Это утверждение — теорема о кинетической энергии.
Если сила совершает положительную работу, то кинетическая энергия тела увеличивается, если работа силы отрицательная, то кинетическая энергия тела уменьшается.
5. Полная механическая энергия ( E ) тела — физическая величина, равная сумме его потенциальной ( E_п ) и кинетической ( E_п ) энергии: ( E=E_п+E_к ) .
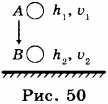
Пусть тело падает вертикально вниз и в точке А находится на высоте ( h_1 ) относительно поверхности Земли и имеет скорость ( v_1 ) (рис. 50). В точке В высота тела ( h_2 ) и скорость ( v_2 ) Соответственно в точке А тело обладает потенциальной энергией ( E_ <п1>) и кинетической энергией ( E_ <к1>) , а в точке В — потенциальной энергией ( E_ <п2>) и кинетической энергией ( E_ <к2>) .
При перемещении тела из точки А в точку В сила тяжести совершает работу, равную А. Как было показано, ( A=-(E_<п2>-E_<п1>) ) , а также ( A=E_<к2>-E_ <к1>) . Приравняв правые части этих равенств, получаем: ( -(E_<п2>-E_<п1>)=E_<к2>-E_ <к1>) , откуда ( E_<к1>+E_<п1>=E_<п2>+E_ <к2>) или ( E_1=E_2 ) .
Это равенство выражает закон сохранения механической энергии: полная механическая энергия замкнутой системы тел, между которыми действуют консервативные силы (силы тяготения или упругости) сохраняется.
В реальных системах действуют силы трения, которые не являются консервативными, поэтому в таких системах полная механическая энергия не сохраняется, она превращается во внутреннюю энергию.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Два тела находятся на одной и той же высоте над поверхностью Земли. Масса одного тела ( m_1 ) в три раза больше массы другого тела ( m_2 ) . Относительно поверхности Земли потенциальная энергия
1) первого тела в 3 раза больше потенциальной энергии второго тела
2) второго тела в 3 раза больше потенциальной энергии первого тела
3) первого тела в 9 раз больше потенциальной энергии второго тела
4) второго тела в 9 раз больше потенциальной энергии первого тела
2. Сравните потенциальную энергию мяча на полюсе ( E_п ) Земли и на широте Москвы ( E_м ) , если он находится на одинаковой высоте относительно поверхности Земли.
1) ( E_п=E_м )
2) ( E_п>E_м )
3) ( E_п
3. Тело брошено вертикально вверх. Его потенциальная энергия
1) одинакова в любые моменты движения тела
2) максимальна в момент начала движения
3) максимальна в верхней точке траектории
4) минимальна в верхней точке траектории
4. Как изменится потенциальная энергия пружины, если её удлинение уменьшить в 4 раза?
1) увеличится в 4 раза
2) увеличится в 16 раз
3) уменьшится в 4 раза
4) уменьшится в 16 раз
5. Лежащее на столе высотой 1 м яблоко массой 150 г подняли относительно стола на 10 см. Чему стала равной потенциальная энергия яблока относительно пола?
1) 0,15 Дж
2) 0,165 Дж
3) 1,5 Дж
4) 1,65 Дж
6. Скорость движущегося тела уменьшилась в 4 раза. При этом его кинетическая энергия
1) увеличилась в 16 раз
2) уменьшилась в 16 раз
3) увеличилась в 4 раза
4) уменьшилась в 4 раза
7. Два тела движутся с одинаковыми скоростями. Масса второго тела в 3 раза больше массы первого. При этом кинетическая энергия второго тела
1) больше в 9 раз
2) меньше в 9 раз
3) больше в 3 раза
4) меньше в 3 раза
8. Тело падает на пол с поверхности демонстрационного стола учителя. (Сопротивление воздуха не учитывать.) Кинетическая энергия тела
1) минимальна в момент достижения поверхности пола
2) минимальна в момент начала движения
3) одинакова в любые моменты движения тела
4) максимальна в момент начала движения
9. Книга, упавшая со стола на пол, обладала в момент касания пола кинетической энергией 2,4 Дж. Высота стола 1,2 м. Чему равна масса книги? Сопротивлением воздуха пренебречь.
1) 0,2 кг
2) 0,288 кг
3) 2,0 кг
4) 2,28 кг
10. С какой скоростью следует бросить тело массой 200 г с поверхности Земли вертикально вверх, чтобы его потенциальная энергия в наивысшей точке движения была равна 0,9 Дж? Сопротивлением воздуха пренебречь. Потенциальную энергию тела отсчитывать от поверхности земли.
1) 0,9 м/с
2) 3,0 м/с
3) 4,5 м/с
4) 9,0 м/с
11. Установите соответствие между физической величиной (левый столбец) и формулой, по которой она вычисляется (правый столбец). В ответе запишите подряд номера выбранных ответов
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Потенциальная энергия взаимодействия тела с Землёй
Б. Кинетическая энергия
B. Потенциальная энергия упругой деформации
ХАРАКТЕР ИЗМЕНЕНИЯ ЭНЕРГИИ
1) ( E=mv^2/2 )
2) ( E=kx^2/2 )
3) ( E=mgh )
12. Мяч бросили вертикально вверх. Установите соответствие между энергией мяча (левый столбец) и характером её изменения (правый столбец) при растяжении пружины динамометра. В ответе запишите подряд номера выбранных ответов.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Потенциальная энергия
Б. Кинетическая энергия
B. Полная механическая энергия
ХАРАКТЕР ИЗМЕНЕНИЯ ЭНЕРГИИ
1) Уменьшается
2) Увеличивается
3) Не изменяется
Часть 2
13. Пуля массой 10 г, движущаяся со скоростью 700 м/с, пробила доску толщиной 2,5 см и при выходе из доски имела скорость 300 м/с. Определить среднюю силу сопротивления, воздействующую на пулю в доске.
17. Механика Читать 0 мин.
Колебания ― это процесс, при котором состояние системы изменяется, повторяясь во времени, и смещаясь то в одну, то в другую сторону относительно состояния равновесия.
Период ― это время, через которое повторяются показатели системы, т. е. система совершает одно полное колебание. Период изменяется в секундах.
Частота ― величина обратная периоду: число полных колебаний за единицу времени. Частота измеряется в герцах [Гц] = [c-1]. Частота равна v = $frac<1>
Если известно, что тело совершает N колебаний за время t, то частоту его колебаний можно определить как v = $frac
N ― количество колебаний;
Для описания колебательных систем, совершающих круговые процессы, удобно использовать круговую (циклическую) частоту. Циклическая частота показывает количество полных колебаний, которые происходят за 2π секунд и равна ω = 2πvили ω = $frac<2pi>
ω ― циклическая частота [рад/с];
Гармонические колебания ― колебания, в которых физические величины изменяются по закону синуса или косинуса. Кинематическое уравнение гармонических колебаний имеет вид:
ω ― циклическая частота [рад/с];
φ0 ― начальная фаза колебаний, [рад];
Смещение (x) ― это отклонение тела от положения равновесия. Смещение также является координатой тела, если отсчитывать ее от положения равновесия.
Амплитуда колебаний (A) ― максимальное отклонение колеблющейся величины от положения равновесия, т. е. максимальное смещение равно амплитуде колебаний xmax = A.
Начальная фаза колебаний (φ0) определяет смещение в начальный момент времени, выраженное в радианах.
Фаза колебаний (φ) или полная фаза колебаний, определяет смещение в данный момент времени, выраженное в радианах. Фаза колебаний равна φ = ωt + φ0, где
φ ― полная фаза колебаний [рад];
φ0 ― начальная фаза колебаний, [рад];
ω ― циклическая частота [рад/с];
Пример анализа гармонических колебаний точки
Рассмотрим гармонические колебания, в которых уравнение движения точки имеет вид x(t) = Asin(ωt), где
ω ― циклическая частота [рад/с].
Из уравнения x(t) = Asin(ωt) следует, что начального смещения нет (φ0 = 0) и колебания начинаются из положения равновесия. Смещение x достигает максимального значения xmax и равно амплитуде xmax = A, в тот момент, когда модуль синуса равен единице |sin(ωt)| = 1. Когда x = A фаза колебаний равна φ = $frac
График колебания координаты точки имеет вид:
Определим уравнение и график колебания скорости. Скорость ― это производная координаты по времени: v = xt‘, где
v ― скорость движения точки [м/с];
Так как закон изменения координаты нам известен x(t) = Asin(ωt), скорость движения колеблющейся точки: v = xt‘ = |Asin(ωt)|’t = Acos(ωt).
Уравнение скорости точки равно v(t) = Acos(ωt), где
v ― скорость движения точки [м/с];
ω ― циклическая частота [рад/с];
Сравнив уравнение v(t) = Aωcos(ωt) с кинематическим уравнением гармонических колебаний, легко заметить, что Aω ― амплитуда изменения скорости, а ωt ― фаза колебаний скорости. Таким образом, максимальное значение скорости равно vmax = Aω, и оно достигается при | cos(ωt) | = 1, т. е. тогда, когда фаза колебаний скорости равна φ = πn, где n = 0, 1, 2, … N.
График колебания скорости точки имеет вид:
Аналогично определяются уравнение и график колебания ускорения точки, которая движется по гармоническому закону.
Ускорение ― это производная скорости по времени: a = vt‘, где
a ― ускорение движения точки [м/с2];
v ― скорость движения точки [м/с];
Так как закон изменения скорости был определен выше v(t) = Aωcos(ωt), определим ускорения движения колеблющейся точки: a = vt‘ = [Aωcos(ωt)]t‘ = –Aω2sin(ωt).
Уравнение ускорения точки равно a(t) = –Aω2sin(ωt), где
a ― ускорение движения точки [м/с2];
ω ― циклическая частота [рад/с];
Модуль ускорения точки максимален, когда |sin(ωt)| = 1 ― тогда же, когда достигает максимума смещение точки. Максимальное ускорение, т. е. амплитуда ускорения точки равна amax = Aω2.
График колебания ускорения точки имеет вид:
Во время гармонических колебаний, формы энергии колебательной системы все время находятся в процессе взаимной трансформации. В механической колебательной системе преобразуется механическая энергия: потенциальная энергия ― в кинетическую, а затем кинетическая энергия ― вновь в потенциальную. Полная механическая энергия колеблющейся системы постоянна, и в любой момент времени справедлив закон сохранения энергии E = EП + EK, где
E ― полная механическая энергия системы, E = const, [Дж];
EП ― потенциальная энергия системы, изменяющаяся во времени, [Дж];
EK ― кинетическая энергия системы, изменяющаяся во времени, [Дж].
Рассмотрим изменение потенциальной энергии пружинного маятника, который колеблется по гармоническому уравнению x(t) = Asin(ωt).
Потенциальная энергия деформированной пружины равна EП = $frac
EП ― потенциальная энергия деформированной пружины, [Дж];
k ― коэффициент упругости пружины [Н/м];
x ― деформация пружины (величина ее удлинения или сжатия) [м].
У пружинного маятника деформация пружины ― переменная величина, которая зависит от времени. Кинематическое уравнение движения точки, принадлежащей этому маятнику ― x(t) = Asin(ωt). Следовательно, потенциальную энергию пружинного маятника можно записать как EП = $frac
Уравнение потенциальной энергии пружинного маятника EП = $frac
EП ― потенциальная энергия пружинного маятника, [Дж];
k ― коэффициент упругости пружины [Н/м];
ω ― циклическая частота [рад/с];
Амплитуда потенциальной энергии пружинного маятника равна EПmax = $frac
EПmax ― максимальная потенциальная энергия пружинного маятника, [Дж];
k ― коэффициент упругости пружины [Н/м];
Потенциальная энергия пружинного маятника равна нулю, когда sin(ωt) = 0 ― когда маятник проходит положение равновесия, и максимальна, когда sin(ωt) = 1 ― когда маятник находится в крайних положениях, т. е. когда его смещение равно амплитуде.
График колебаний потенциальной энергии пружинного маятника:
Рассмотрим изменение кинетической энергии маятника. Кинетическая энергия тела равна Eк = $frac
Eк ― кинетическая энергия тела, [Дж];
v ― скорость движения тела, [м/с].
У тела, которое совершает колебательные движения, скорость ― переменная величина.
Выше было показано, что если уравнение движения точки имеет вид x(t) = Asin(ωt), то уравнение скорости точки v(t) = Aωcos(ωt). Таким образом, кинетическая энергия маятника равна Eк = $frac
Уравнение кинетической энергии маятника Eк = $frac
Eк ― кинетическая энергия маятника, [Дж];
ω ― циклическая частота [рад/с];
Амплитуда кинетической энергии маятника равна EКmax = $frac
EКmax ― максимальная кинетическая энергия маятника, [Дж];
ω ― циклическая частота [рад/с].
Максимальная кинетическая энергия маятника достигается тогда, когда cos2(ωt) = 1 ― маятник проходит положение равновесия, и она равна нулю, когда маятник находится в крайнем положении.
График колебаний кинетической энергии маятника:
Математический маятник ― это колебательная система, состоящая из материальной точки, подвешенной на нерастяжимой нити или стержне.
Период колебаний математического маятника равен T = $2pi sqrt
l ― длина нити математического маятника [м];
g ― ускорение свободного падения [м/с2].
Период колебаний пружинного маятника равен T = $2pi sqrt
Существует особый тип колебаний ― вынужденные колебания. Вынужденные колебания происходят только под постоянным периодическим внешним воздействием и их характеристики зависят от характеристик этого воздействия.
Если частота внешнего воздействия, которое вызывает вынужденные колебания, совпадает с собственной внутренней частотой колебательной системы ― возникает явление резонанса. При резонансе резко возрастает амплитуда колебаний системы. Частота, при которой возникает явление резонанса, называется резонансной частотой.
На рисунке показан график резонансной кривой ― увеличение амплитуды при совпадении частоты внешнего воздействия с внутренней частотой системы.