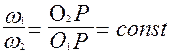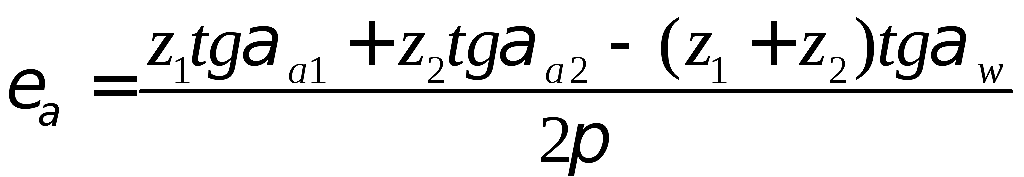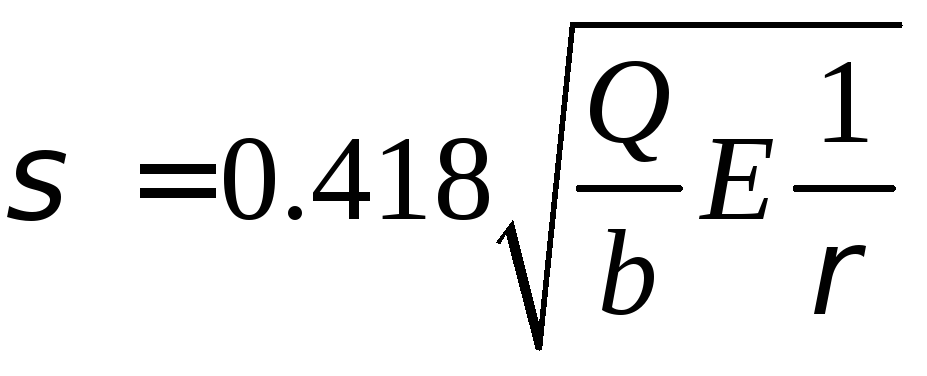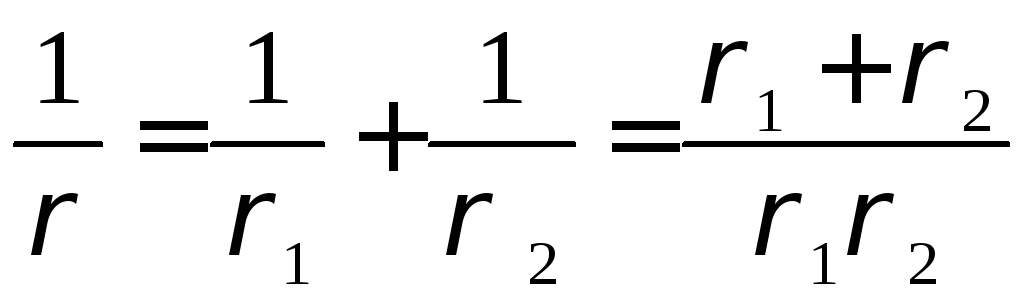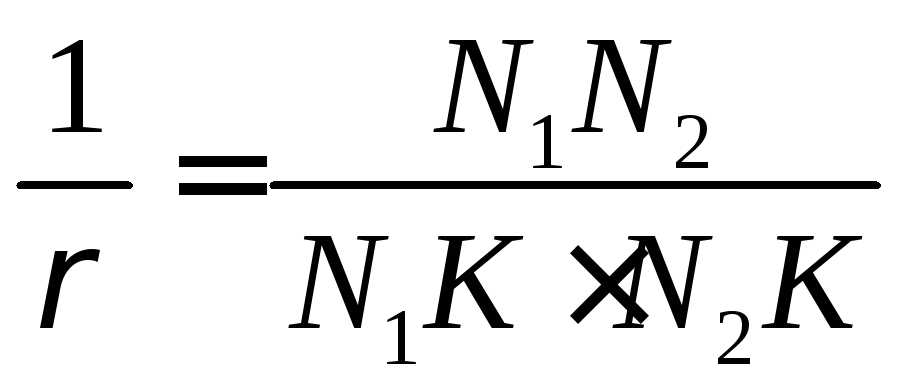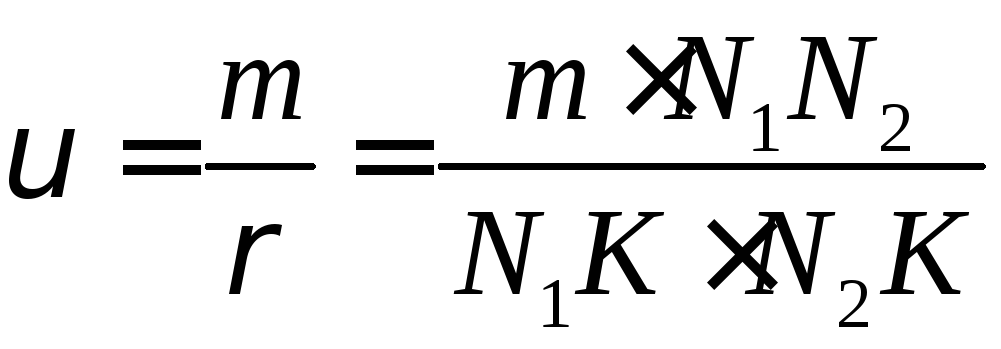Как определить передаточное отношение зубчатой…

Передаточное отношение. Передаточное отношение зубчатой передачи

Рассматривая тему деталей машин, нельзя не уделить внимания такому важному техническому показателю, как передаточное отношение. Этот термин существует уже достаточно давно и о его значении в механике стоит поговорить отдельно.

Формулировка

Передаточное отношение – одна из самых важных технических характеристик любой механической передачи вращательного движения. С практической точки зрения, описываемый показатель позволяет понять, во сколько раз вырастает момент силы в результате функционирования передачи. Определение передаточных отношений в любом механизме – одна из самых главных задач в механике и машиностроении.

Некоторые тонкости

Передаточное отношение определяется при наличии как минимум двух зубчатых колес (шестерен), которые находятся в зацеплении между собой. Такое сопряжение именуется зубчатой передачей.

Самый простой способ рассчитать передаточное число – посчитать количество зубьев на каждом из имеющихся колес, а после произвести деление числа зубьев ведомой шестерни на количество колес ведущей шестерни. Данное рациональное число и будет являться передаточным отношением.

Важно иметь в виду, что в случае определения передаточного числа в зубчатой передаче, имеющей несколько шестерен, необходимо опять-таки делить количество зубьев ведущего колеса на количество ведомого. При этом параметры промежуточных шестерен не учитываются.

Обзор передач

На сегодняшний день существуют такие виды механических передач:

• Зубчатые.
• Ременные.
• Фрикционные.
• Червячные.
• Цепные.
• Храповые.
• Волновые.

В целом же, механические передачи разделяются по таким критериям:

• В зависимости от передачи движения от ведущего звена к ведомому: передачи трением и передачи зацеплением.
• В зависимости от соотношения скоростей ведомого и ведущего звеньев: замедляющие передачи (они же редукторы), ускоряющие передачи (мультипликаторы).
• В зависимости от расположения осей валов: передачи с перекрещивающимися, пересекающимися и параллельными осями.

Стоит указать, что замедляющие передачи на практике применяются гораздо чаще, нежели ускоряющие. Этот факт объясняется тем, что скорости вращения двигателей зачастую гораздо выше требуемой скорости вала исполнительного механизма или машины.

Зубчатая передача

Передаточное отношение зубчатой передачи можно вычислять не только по соотношению зубьев ее колес, но также путем деления значения угловой скорости ведомого вала на угловую скорость ведущего вала, а также благодаря соотношению числа оборотов ведомого и ведущего валов.

Диапазон передаточного отношения может быть очень велик и достигать больших значений. При этом само по себе передаточное отношение зубчатой передачи характеризуется постоянством, так как зацепление не подвержено проскальзыванию. Коэффициент полезного действия такой передачи находится в пределах 0,97-0,98.

Зубчатые передачи передают вращение между валами, которые могут иметь параллельные, скрещивающиеся или перпендикулярные оси. Кроме того, такие передачи способны трансформировать (преобразовывать) поступательное движение во вращательное и наоборот (передчи «винт-гайка»).

Зацепление в зубчатых передачах может быть как внешним, так и внутренним. Колеса изготавливаются с прямыми, косыми или шевронными зубьями.

Зубчатые передачи способны передавать большие скорости вращения с постоянным передаточным отношением и имеют высокий КПД.

Передаточное отношение редуктора является одним из важнейших критериев в процессе его выбора. Вторым по важности показателем считается межосевое расстояние.

Червячная передача

Используется для передачи вращательного движения в тех случаях, когда оси валов перекрещиваются.

Червяк может быть цилиндрическим или глобоидным в зависимости от поверхности расположения резьбы, а также может быть эвольвентным или архимедовым (в данном случае решающую роль играет профиль резьбы).

Основными недостатками описываемой передачи можно считать:

• Высокий показатель тепловыделения.
• Частое заедание и невысокий КПД.

Волновая передача

Ее работа основывается на принципе трансформации параметров движения благодаря волновому деформированию гибкого элемента механизма. По сути, такая передача является разновидностью планетарной передачи.

В состав волновой передачи входит жесткое колесо зубчатое, имеющее внутренние зубья, и вращающееся гибкое колесо с наружными зубьями. Оба колеса между собой входят в зацепление благодаря генератору волн, соединенному непосредственно с корпусом передачи.

За счет имеющихся конструктивных особенностей волновая передача наделена следующими достоинствами:

• Небольшие габариты и масса.
• Высокая кинематическая точность.
• Передаточное отношение передачи в одной ступени имеет большой показатель и вполне может достигать 300.
• Идеальная демпфирующая способность.
• Формирование в одной ступени большого передаточного отношения.

К недостаткам же относятся:

• Весьма сложная конструкция.
• Высокие потери мощности на трение и деформацию гибкого колеса (КПД составляет порядка 0,7-0,85).

Фрикционная передача

Чаще всего применяется в текстильной отрасли, станкостроении и прочих сферах промышленности, кроме авиастроения. Передаваемая мощность может достигать 10 кВт. При больших показателях очень трудно гарантировать требуемое усилие прижатия катков.

В передаче существует три вида скольжения: геометрическое, упругое и буксование.

Для нормально функционирующей передачи характерно именно упругое скольжение, в то время как буксование говорит о наличии перегрузки.

Ременная передача

Как и зубчатая она встречается очень часто. В зависимости от того, как располагаются валы и ремень, передача может быть:

• Открытой.
• Перекрестной.
• Полуперекрестной.
• Угловой.
• Спаренной.
• Ступенчатой.

Ремень может быть круглым, плоским, трапецеидальным.

Передаточное отношение в таких передачах находится в пределах 1:4, 1:5 и лишь в редких случаях может быть равно 1:8.

К положительным качествам ременной передачи следует отнести:

• Простоту конструкции.
• Возможность расположения обоих шкивов на большом расстоянии друг от друга (свыше 15 метров).
• Бесшумность и плавность работы.
• Защиту механизмов от перегрузок благодаря упругим свойствам ремня и его способности в определённые моменты проскальзывать по поверхностям шкивов.
• Работу при больших угловых скоростях.

Недостатками передачи являются:

• Удлинение ремней (их вытягивание) в процессе работы, то есть недолговечность.
• Непостоянство передаточного числа, что объясняется неизбежным проскальзыванием ремня.
• Достаточно большие размеры.

Цепная передача

В отличие от ременного аналога не подвержена проскальзыванию. Расчет передаточного отношения выполняется по аналогии с зубчатой передачей, ведь звездочки передачи, по сути, представляют собой те же зубчатые колеса.

Характерная особенность цепной передачи – вращение передается исключительно при наличии параллельных валов. Между осями звёздочек расстояние необходимо принимать не менее величины полутора диаметров большой звездочки. При этом передаточное число может достигать показателя 1:15.

Также важно заметить, что цепь надевается на звездочки не с натягом, как ремни, а с определенной степенью провисания. Регулировка натяжения проводится с помощью специального винта.

Достоинства передачи таковы:

• Небольшая чувствительность к неточностям установки валов.
• Передача вращения может осуществляться одной цепью сразу же нескольким звездочкам.
• Вращение может передаваться на большие расстояния.

Недостатком же является высокий шум и износ цепей в случае некачественного монтажа и при плохом техническом обслуживании.

Храповый механизм

Во многих машинах и агрегатах применяется не только непрерывное вращательное движение, но и прерывистое тоже, которое осуществляется с помощью храповика, собачки и рычага.

Храповый механизм помимо вращения еще и осуществляет предохранительную функцию. Так, например, в грузоподъемных лебедках, храповик совместно с собачкой не позволяют барабану проворачиваться в обратную сторону, надёжно фиксируя его в требуемом пространственном положении.

Рассмотренные виды механических передач применяются практически в любой отрасли народного хозяйства и получили широчайшее распространение благодаря своим техническим возможностям.

Как определить передаточное отношение зубчатой…

• Главная
• Категории
• Технологии
• Расчет передаточного отношения и частоты вращения.

Расчет передаточного отношения и частоты вращения.

• Печать
• E-mail

Как рассчитать передаточное отношение шестерен механической передачи.

В этой статье я приведу пример расчета передаточного отншения шестерен разного диаметра, с разным количеством зубьев. Данный расчет применяется в том случае, когда важно определить к примеру скорость вращения вала редуктора при известной скорости привода и характеристиках зубьев.

Естественно, можно произвести замеры частоты вращения выходного вала, однако в некоторых случаях требуется именно расчет. Помимо этого, в теоретической механике, при конструировании различных узлов и механизмов требуется рассчитать шестерни, чтобы получить заданную скорость вращения.

Термин передаточное число является весьма неоднозначным. Он перекликается с термином передаточное отношение, что не совсем верно. Говоря о передаточном числе, мы подразумеваем сколько оборотов совершит ведомое колесо (шестерня) относительно ведущего.

Для правильного понимания процессов и строения шестерни – следует предварительно ознакомится с ГОСТ 16530-83.

Итак, рассмотрим пример расчета с использованием двух шестерен.

Чтобы рассчитать передаточное отношение мы должны иметь как минимум две шестерни. Это называется зубчатая передача. Обычно первая шестерня является ведущей и находится на валу привода, вторая шестерня называется ведомой и вращается входя в зацепление с ведущей. Пи этом между ними может находится множество других шестерен, которые называются промежуточными. Для упрощения расчета рассмотрим зубчатую передачу с двумя шестернями.

В примере мы имеем две шестерни: ведущую (1) и ведомую (2). Самый простой способ заключается в подсчете количества зубьев на шестернях. Посчитаем количество зубьев на ведущей шестерне. Так же можно посмотреть маркировку на корпусе шестерни.

Представим, что ведущая шестерня (красная) имеет 40 зубьев, а ведомая(синяя) имеет 60 зубьев.

Разделим количество зубьев ведомой шестерни на количество зубьев ведущей шестерни, чтобы вычислить передаточное отношение. В нашем примере: 60/40 = 1,5. Вы также можете записать ответ в виде 3/2 или 1,5:1.

Такое передаточное отношение означает, что красная, ведущая шестерня должна совершить полтора оборота, чтобы синяя, ведомая шестерня совершила один оборот.

Теперь усложним задачу, используя большее количество шестерен. Добавим в нашу зубчатую передачу еще одну шестерню с 14 зубьями. Сделаем ее ведущей.

Начнем с желтой, ведущей шестерни и будем двигаться в направлении ведомой шестерни. Для каждой пары шестерен рассчитываем свое передаточное отношение. У нас две пары: желтая-красная; красная-синяя. В каждой паре рассматриваем первую шестерню как ведущую, а вторую как ведомую.

В нашем примере передаточные числа для промежуточной шестерни: 40/14 = 2,9 и 60/40 = 1,5.

Умножаем значения передаточных отношений каждой пары и получаем общее передаточное отношение зубчатой передачи: (20/7) × (30/20) = 4,3. То есть для вычисления передаточного отношения всей зубчатой передачи необходимо перемножить значения передаточных отношений для промежуточных шестерен.

Определим теперь частоту вращения.

Используя передаточное отношение и зная частоту вращения желтой шестерни, можно запросто вычислить частоту вращения ведомой шестерни. Как правило, частота вращения измеряется в оборотах в минуту (об/мин) Рассмотрим пример зубчатой передачи с тремя шестернями. Предположим, что частота вращения желтой шестерни 340 оборотов в минуту. Вычислим частоту вращения красной шестерни.

Будем использовать формулу: S1 × T1 = S2 × T2,

S1 – частота вращения желтой (ведущей) шестерни,

Т1 – количество зубьев желтой (ведущей) шестерни;

S2- частота вращения красной шестерни,

Т2 – количество зубьев красной шестерни.

В нашем случае нужно найти S2, но по этой формуле вы можете найти любую переменную.

340 rpm × 7 = S2 × 40

Получается, если ведущая, желтая шестерня вращается с частотой 340 об/мин, тогда ведомая, красная шестерня будет вращаться со скоростью примерно 60 об/мин. Таким же образом рассчитываем частоту вращения пары красная-синяя. Полученный результат – частота вращения синей шестерни – будет являться искомой частотой вращения всей зубчатой передачи.

Определение передаточных отношений зубчатых механизмов.

Передаточное число зубчатой передачи определяется по формуле:

где и — числа зубьев колес 1 и 2, соответственно.

Знак «+» берется для внешнего зацепления (рис.1 и рис.2), знак «–» для внутреннего зацепления. Виды зацеплений приведены на рис.2. Знаки учитываются только для зубчатых передач с параллельными осями вращения колес.

Общее передаточное число (отношение) зубчатой передачи при последовательном соединении ступеней равно произведению передаточных чисел входящих в них ступеней.

Передаточное число планетарного механизма определяется по формуле:

где — передаточные числа ступеней (с учетом знаков) при остановленном водиле.

Кинематика кулисного механизма.

Выбираем масштаб:

Скорость точки :

Относительная скорость звеньев 3 и 2:

Модули абсолютной скорости точки цилиндра:

Основная теорема зацепления.

Общая нормаль к профилям зубчатых колес, находящимся в зацеплении, делит межосевое расстояние на части, обратно пропорциональные угловым скоростям, т.е.,

где О_1, О₂ – центры вращения соответственно шестерни и зубчатого колеса; Р – полюс зацепления.

Для доказательства основной теоремы рассмотрим зацепление двух зубьев в некоторый момент времени в точке М со скоростями этих точек и . Проведем через точку касания М общие касательную ТТ и нормаль nn. Очевидно, что условием непрерывности зацепления при вращении колес будет равенство проекций скоростей на общую нормаль . Обозначая углы векторов с нормалью через и имеем ,

Качественные показатели зубчатых передач.

Коэффициент перекрытия учитывает непрерывность и плавность зацепления в передаче. Такие качества передачи обес­печиваются перекрытием работы одной пары зубьев работой дру­гой пары. Для этого каждая последующая пара зубьев должна войти в зацепление еще до того, как предшествующая пара выйдет из зацепления. О величине перекрытия судят по коэффициенту перекрытия, который выражают отношением угла торцового перекрытия к угловому шагу. Угол торцового перекрытия это угол поворота колеса от положения зубьев при входе в зацепление, когда они касаются в точке В ’ , до положения зубьев при выходе из зацепления, когда они касаются в точке B » . Сле­довательно, коэффициент перекрытия прямозубой передачи

Коэффициент скольжения учитывает влияние гео­метрических и кинематических факторов на величину проскальзы­вания профилей в процессе зацепления. Наличие сколь­жения при одновременном нажатии одного профиля на другой при­водит к износу профилей. Коэффициенты скольжения выражаются формулами:

где — скорость скольжения; и — скорости перемеще­ния точек контакта по профилям зубьев первого и второго колеса.

Коэффициент удельного давления учитывает влияние геометрии зубьев (радиусов кривизны их профилей) на величину контактных напряжений, возникающих в местах сопри­косновения зубьев. При чрезмерном нагружении контактные напря­жения могут быть столь значительны, что вызовут выкрашивание материала на рабочей поверхности зубьев.

Контактные напряжения определяются по формуле Герца:

где Q— сила взаимодействия зубьев; b— ширина зубчатых ко­лес;

E = 2E₁E₂/( E₁ + E₂)— приведенный модуль упругости их мате­риалов; ρ- приведенный радиус кривизны эвольвентных профилей в точке контакта, посредством которою определяется влияние геометрии зуба на контактные напряжения.

Для текущего момента зацепления зубьев:

или, согласно свойствам эвольвентных профилей:

Коэффициентом удельного давления u называется отношение:

Коэффициент u — величина безразмерная, не зависящая от модуля m, так какпропорцио­нален модулю.