Как изготовить шестерню по образцу своими руками
Одной из самых сложных и, тем не менее, распространенных механических систем является зубчатая передача. Это отличный способ передачи механической энергии из одного места в другое и способ увеличения или уменьшения мощности (крутящего момента), а также увеличения или уменьшения скорости чего-либо.
Как сделать шестеренку своими руками? Проблема всегда заключаются в том, что для создания эффективных зубчатых колес требуется достаточно много навыков рисования и знание математики, а также умение создавать сложные детали.
Для любительского нет необходимости иметь максимальную эффективность, поэтому мы можем получить намного более легкую в изготовлении систему, даже с подручными инструментами.
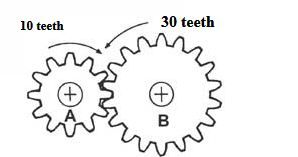
Шестерня — это ряд зубьев на колесе. (Обратите внимание на диаграмму выше, они пометили неправильное количество зубьев на шестернях — извините)
Шаг 1: Формулы и расчеты
Формулы для рисования и изготовления зубьев зубчатых колес в избытке можно найти в интернете, но для новичка они кажутся очень сложными.
Я решил упростить задачу, и решение очень хорошо работает как в больших, так и в малых масштабах. В небольших масштабах это лучше всего подходит для машинной резки с помощью лазерных резаков, например, очень маленькие зубчатые колеса могут быть успешно изготовлены таким образом.
Шаг 2: Простой способ
Итак, форма зубца, если говорить просто, может представлять собой полукруг.
Шаг 3: Определяем размеры
Теперь мы можем определить параметры, чтобы сделать шестерню:
- Насколько большими / маленькими будут зубья шестерни (диаметр) — чем меньше шестерня, тем меньше должны быть зубья.
- Все зубья, которые собираются в сцепление (соединяются), должны быть одинакового размера, поэтому сначала нужно рассчитать меньшую шестерню.
Давайте начнем с зубьев размером 10 мм.
Я хочу шестерню с 5 зубьями, чтобы круг был 10х10 мм (в окружности) = 100 мм.
Чтобы нарисовать этот круг, мне нужно найти диаметр, поэтому я использую математику и калькулятор и делю окружность (100 мм) на Pi = 3,142.
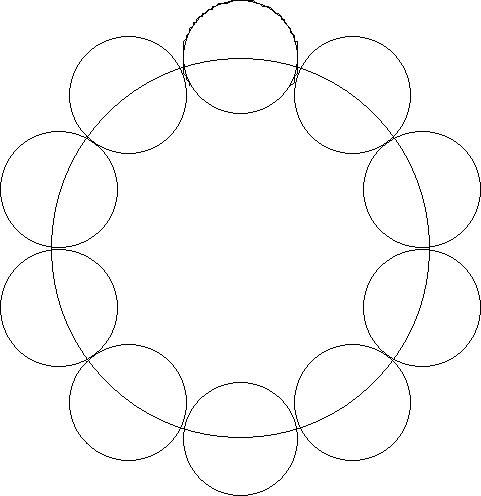
Это дает мне диаметр 31,8 мм, и я могу нарисовать этот круг с помощью циркуля, а затем нарисовать с помощью циркуля на его окружности ровно 10 кругов диаметром 10 мм.
Если у вас есть такая возможность, то проще сделать все с помощью программного обеспечения для рисования. Если вы используете программное обеспечение, вы должны иметь возможность вращать круги зубьев вокруг основного круга, и вам нужно будет знать, как далеко повернуть каждый зуб. Это легко рассчитать: делите 360 градусов на количество кругов. Таким образом, для наших 10 кругов 360/10 = 36 градусов для каждого зуба.
Шаг 4: Делаем зубчатую форму
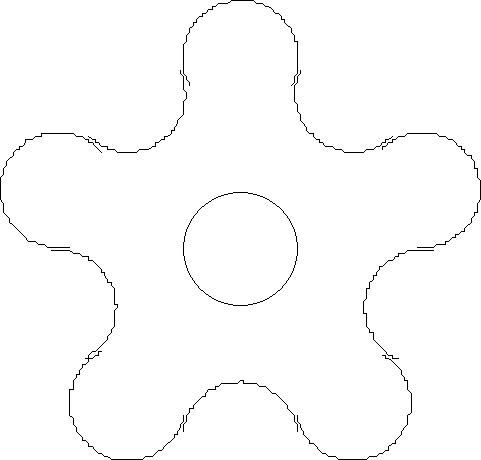
Удалите верхнюю часть одного круга и нижнюю часть следующего круга. Чтобы сделать это, у вас должно быть четное количество зубьев
У нас есть первая шестерня. Она может быть вырезана из дерева или металла с помощью базовых подручных инструментов, пил и напильников.
Этот процесс легко повторить для любого количества шестеренок, которое вам нужно. Держите размер круга по образцу, и они будут соответствовать друг другу.
Шаг 5: Получите шестерёнку
Поскольку такие полукруглые шестеренки легко вырезать, вы можете сделать их с помощью подручного инструмента и лобзика или пилы.
Раньше я делал шаблон из 9 или 10 зубьев на фанере и использовал его в качестве ориентира для моего ручного фрезера и без проблем вырезал шестерни.
Если у вас есть доступ к лазерному резцу, они могут быть вырезаны из акрила 3 или 5 мм толщины и быть очень маленьких размеров.
Рассказываю как сделать какую-либо вещь с пошаговыми фото и видео инструкциями.
Техническое черчение
Эвольвентный профиль зубца. Построение эвольвенты в общем виде было рассмотрено в главе „Геометрическое черчение». Рассмотрим практическое применение этой кривой при вычерчивании профиля зубцов зубчатых колёс. Пусть даны два цилиндрических зубчатых колеса с модулем m=18 и числом зубцов: первого z1 = 18, второго z2 = 12.
Для вычерчивания профиля зубцов пользуемся ранее приведёнными формулами. Находим размеры элементов зубцов.
d1 = m • z1 = 18 • 18 = 324 мм; De1 = m (z1 + 2) = 18(18 + 2) = 360 мм;
Di1= De1 — 2 • 2,2 m = 360 — 2 • 2,2 • 18 = 280,8 мм; t= ? • m = 3,14 • 18 = 56,52 мм.
d2 = m • z2 = 18 • 12 = 216 мм; De2 = m (z2 + 2) = 18 (12 + 2) = 252 мм;
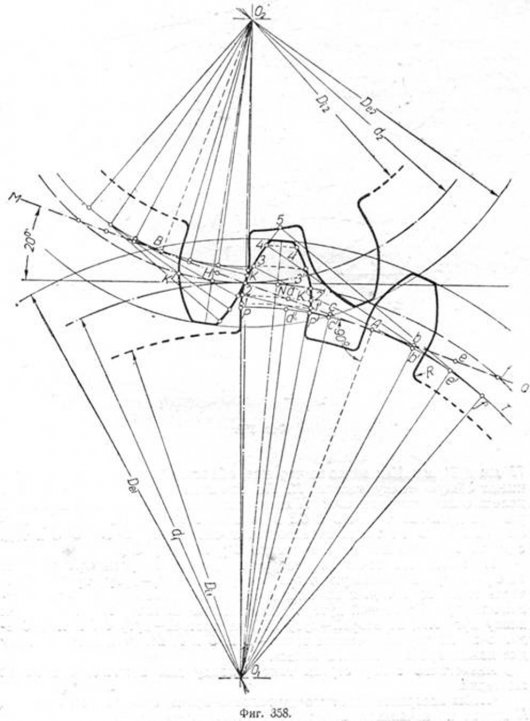
Проводим из центров O1 и 02 (фиг. 358) начальные окружности, окружности выступов и окружности впадин, обращая при этом внимание на то, чтобы начальные окружности обоих колёс имели одну общую точку касания К, лежащую на линии центров O1—O2. Далее через точку К проводим под углом 20° к общей касательной начальных окружностей прямую MQ и, опустив из центров О1 и 02 на эту прямую перпендикуляры, получим точки А и В. Из центра О1 радиусом О1А описываем основную окружность (на чертеже показана только часть её). Делим прямую KA на равное число частей, например на три, и отметим точки деления буквами d, с и вправо от точки А —b, e, f.
Затем откладываем от точки А влево и вправо эти отрезки по дуге основной окружности PAT; точки деления обозначаем буквами d’, с’, b’, е’у f ‘ и соединяем их радиусами с центром О1.
Проводим через точки d’, c’, b’, e’, f’ перпендикулярно к радиусам лучи. Далее на этих лучах откладываем отрезки: на луче d’—отрезок AC, получим точку 1; на луче с’—отрезок Ad, получим точку 2 и т. д. Соединив по лекалу найденные таким образом точки 1, 2, 3, 4, 5, получим эвольвенту, по которой должен быть вычерчен профиль зубца большего колеса.
Аналогичным построением получим профиль зубца и для второго колеса.
Чтобы вычертить полный профиль зубца, откладываем по дугам начальных окружностей от точки К вправо и влево размер толщины зубца s = KK’. Делим s пополам и через середины зубцов, отмеченные точками N и H, проводим прямые O1N и 02H, а затем из центра 01 описываем ряд дуг: 1-1′; 2—2′; 3—3′ и т. д. Эти дуги делятся прямой 01N пополам. Проводя таким образом дуги из центра 02, легко построим полный профиль зубца и для второго колеса. Следует заметить, что по эвольвенте вычерчивается часть зубца—кривая PK5, которая начинается от точки Я, лежащей на основной окружности. Нижняя часть зубца вычерчивается по прямой, имеющей направление от точки P к центру O1. Место примыкания ножки зубца к окружности впадин скругляется радиусом R = 0,2 m. В нашем примере R = 3,6 мм.
Циклоидальный профиль зубца. Образование профиля зубца колеса производится по кривым—эпициклоиде и гипоциклоиде.
Пусть дано: модуль m = 16, число зубцов первого колеса z1 = 12, второго — z2 = 8. Для построения зубцов цилиндрических колёс определим сначала их конструктивные элементы.
Диаметры начальных окружностей
Диаметры окружностей выступов
De1 = m (z1+ 2) = 224 мм; De2 = m (z2 + 2) == 160 мм. Диаметры окружностей впадин
s = 0,487 *t = 24,47 мм,
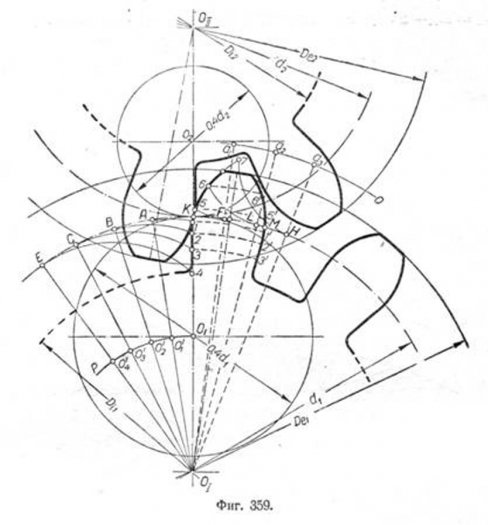
Строим из центров OI и ОII(фиг. 359) начальные окружности, окружности выступов и впадин. Из точек 01 й 02 описываем вспомогательные окружности, диаметры которых соответственно равны 0,4 d1 и 0,4 d2 т. е.
77 мм и 51 мм. Как видно из чертежа, обе вспомогательные окружности имеют общую точку касания К. По начальной окружности большого колеса откладываем от точки К влево равные по величине произвольного размера дуги KA, AB, ВС и СЕ и из центра 0I радиусом 0I —О1 описываем дугу ОI Р. Точки пересечения лучей 0IA, ОIВ, 0IС и т.д. с дугой О1Р отмечаем соответственно 0′1 0′2, 0′3, 0′4.
Принимая эти точки за центры, проводим радиусом О1К ряд дуг: из O1‘—дугу, проходящую через точку Л, из 0’2 — дугу, проходящую через точку В, и т. д. и на этих дугах откладываем длины соответствующих дуг. На первой дуге, проходящей через точку A, откладываем длину дуги AK, на второй—дугу BK, на третьей—дугу CK и т. д. Соединив по лекалу полученные точки—1, 2, 3 и 4, получим гипоциклоиду для ножки зубца большого колеса.
Аналогично этому строим гипоциклоиду для ножки зубца малой шестерни.
Чтобы построить эпициклоиду головки зубца, откладываем от точки К вправо по начальной окружности этого колеса несколько равных по величине произвольного размера дуг KF, FL, LH и проводим из центра OI радиусом 0I—02 дугу 02Q. Пересечения лучей 0I, F, 01 L u OIH дадут на проведённой дуге точки a1, а2 и а3. Принимая эти точки за центры, проводим радиусом O2K из точки а1 дугу, проходящую через точку F.
из а2—дугу через L и т.д. Отложив затем на первой дуге длину дуги FK, получим точку 5, на второй дуге—длину дуги LK, получим точку 6 и т. д. Соединив точки К, 5, 6 и 7 по лекалу до пересечения с окружностью выступов большего колеса, получим эпициклоиду головки.
Чтобы построить полный профиль этого зубца, необходимо по начальной окружности большего колеса отложить толщину зубца s = 24 мм, равную КМ, разделить её пополам (на чертеже середина отмечена штрих-пунктирной линией, выходящей из OI ) и затем симметрично построить, справа от этой линии, точки 3′, 2′, 1′, 5′, 6′ и т. д.
Построение профиля головки зубца малого колеса производится аналогично построению зубца большего. Для вычерчивания остальных зубцов следует разделить начальные окружности на равное число частей, соответственно числу зубцов шестерни. Расстояние между центрами каждых двух смежных зубцов по дуге начальной окружности должно равняться шагу зацепления t.
Упрощённый способ вычерчивания профиля зубца. Этот способ применяется для вычерчивания эвольвентного профиля зубцов зубчатых
колёс с литыми зубцами, а также для указания обработки, размеров элементов зубца на рабочем чертеже зубчатого колеса и т. п. Рассмотрим это построение на примере.
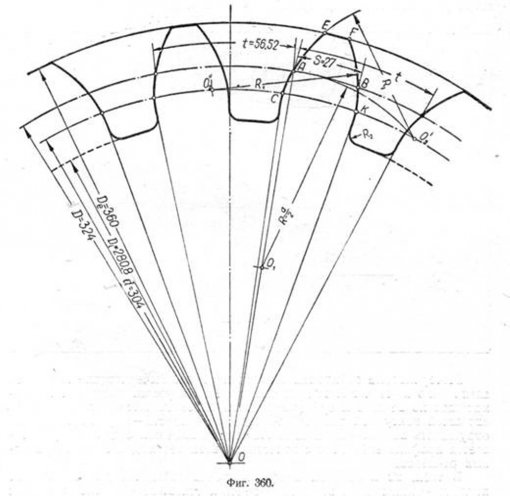
Пусть даны: d = 324 мм, De = 360 мм, Di=280,8 мм, m=18, z=18, шаг t=56,52 мм и s=27мм; требуется вычертить профиль зубца (фиг. 360). Из центра 0 зубчатого колеса проводим дуги окружностей диаметров d, De и Di . Определяем диаметр основной окружности по формуле: D = d cos 20° = 324-0,94 = 304 мм и строим её. Намечаем на начальной окружности произвольную точку А и откладываем толщину зубца s = 27 мм = АВ. Соединяем точку А с центром 0 и, разделив OA пополам, получим центр O1 Радиусом R, равным OA/2 = d/2 из центра О1 описываем дугу до пересечения с основной окружностью в точке 02. Из этой
точки радиусом R1 проводим дугу CAE, Сделав из точки В на основной окружности засечку тем же радиусом R1 получим точку 02«, из которой описываем дугу ВК. Точки САЕFВК принадлежат очертанию головки зубца. Ножка зубца строится по прямым линиям, имеющим направление от точек А и В к центру О. Сопряжение линий профиля ножки с окружностью впадин выполняется радиусом R2, равным 0,2 m. Профиль остальных зубцов строится аналогичным способом. Откладываем по начальной окружности шаг t и толщину зубца s, затем радиусом R1 строим головку зубца и т. д.
Вычерчивание звёздочек цепных передач. Вычерчивание звёздочек аналогично вычерчиванию зубчатых колёс. Наружная окружность, проходящая по вершинам зубьев звёздочки, вычерчивается на главном виде сплошной контурной линией, начальная окружность-штрих-пунктирной, окружность впадин—штриховой. На том же виде или отдельно вычерчивается профиль звёздочки с нанесением всех необходимых конструктивных размеров.
В табл. 22 приведены профили зубьев звёздочек для приводных втулочно-роликовых и втулочных цепей и основные зависимости для их построения.
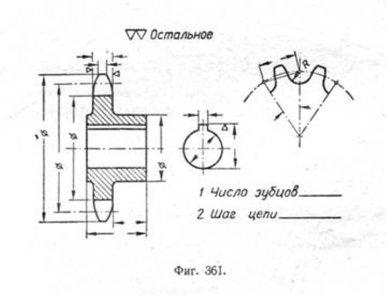
В табл. 23 приведены данные для звёздочек зубчатых цепей. На фиг. 361 дан конструктивный чертёж звёздочки для втулочно-роликовой цепи.
Создание шестерни в Компас-3D
В этом уроке мы научимся создавать зубчатые колеса. Зубчатое колесо (шестерня) является основной деталью зубчатой передачи в виде диска с зубьями и предназначена для передачи вращения между валами. Различают 2 основных вида зубчатых колес – цилиндрические (прямозубые, косозубые, шевронные, с круговыми зубьями и др.) и конические (с круговым (винтовым) и прямым зубом). Построить профиль шестерни обычными инструментами Компас-3D, такими как выдавливание и вырезание выдавливанием является проблематичным, так как профиль зуба шестерни строится по сложной кривой – эвольвенте.
Видеокурс по этой теме
Видеокурс «Основы конструирования в КОМПАС-3D v19»
Видеокурс направлен на освоение основ конструирования в САПР КОМПАС-3D. Обучение проводится на примере создания моделей узлов и сборки из них промышленного прибора, разбор особенностей моделирования и визуализации результатов в…
alt=»Создание шестерни в Компас-3D» width=»697″ height=»424″ />Эвольвентное зацепление шестерен
Для этих целей в Компас-3D существует библиотека Валы и механические передачи, которая находится в меню приложения – механика.
В качестве примера возьмем косозубое колесо с числом зубьев z=55, модулем m=10 и углом наклона =15°13′21″.
При запуске библиотеки, слева появляется панель основных настроек будущей шестерни, такими как вид зацепления, размеры фасок, параметры отображения модели и таблица с параметрами зубьев. Выбор между построением ведущего и ведомого колеса осуществляется кнопкой сменить элемент . Для редактирования параметров зубьев нажмем кнопку Расчет в модуле “КОМПАС-GEARS” и в появившемся меню выберем геометрический расчет. В Открывшейся таблице установим требуемые значения для ведущего колеса и если требуется – для ведомого колеса на вкладке страница 1 и перейдем на вкладку страница 2.
alt=»Создание шестерни в Компас-3D» width=»840″ height=»723″ /> Страница 1 геометрического расчета
На этой вкладке также откорректируем значения, если требуется. Для начала расчета нажмем кнопку Расчёт, после чего программа произведет расчеты и укажет на возможные ошибки, либо их отсутствие в нижней части окна.
alt=»Создание шестерни в Компас-3D» width=»841″ height=»726″ /> Страница 2 геометрического расчета
На этой странице также можно записать полученные данные в отдельный файл либо просмотреть данные в отдельном окне. Кнопка визуализации зацепления доступна только в режиме двухмерного создания. Для завершения расчетов и переходу к построению модели нужно нажать закончить расчеты. Теперь, после закрытия окна построения зубьев, можно добавить корректировки в основных параметров шестерни и нажать OK
alt=»Создание шестерни в Компас-3D» width=»680″ height=»501″ /> Получившаяся модель зубчатого колеса
Получилась модель шестеренки с заданными модулем, диаметром, углом наклона зубьев и др. Теперь можно перейти к построению остальных элементов колеса: отверстий, шлицов, канавок и прочих элементов предусмотренных конструкцией.
Кроме зубцов, в зубчатых колесах используются отверстия или валы (вал-шестерни) со шпоночными или шлицевыми соединениями, созданными в соответствии с действующими ГОСТами, для передачи вращения. Эти элементы также создаются в библиотеке Компас-Gears, но более подробно о их создании будет рассказано в уроке “Механические передачи в Компас-3D”
Создание конической модели шестерни производится аналогично, различие заключается только выборе библиотеки, вместо цилиндрической нужно выбрать коническую.
alt=»Создание шестерни в Компас-3D» width=»1072″ height=»553″ /> Путь к библиотеке для конических зубчатых колес
После чего также запустить окно модуля “КОМПАС-GEARS” и ввести данные своей конической шестерни.
alt=»Создание шестерни в Компас-3D» width=»764″ height=»602″ /> Окно ввода параметров для построения конической шестерни
Дальнейшие действия аналогичны как при построении цилиндрического зубчатого колеса.