Емкость конденсаторов: определение, формулы, примеры.
Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.
Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:
C = q φ 1 — φ 2 = q U .
Значением φ 1 — φ 2 = U обозначают разность потенциалов, называемую напряжением, то есть U . По определению емкость положительна. Она зависит только от размерностей обкладок конденсатора их взаиморасположения и диэлектрика. Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным. Конденсатор может являться проводником, помещенным в полость, окруженным замкнутой оболочкой.
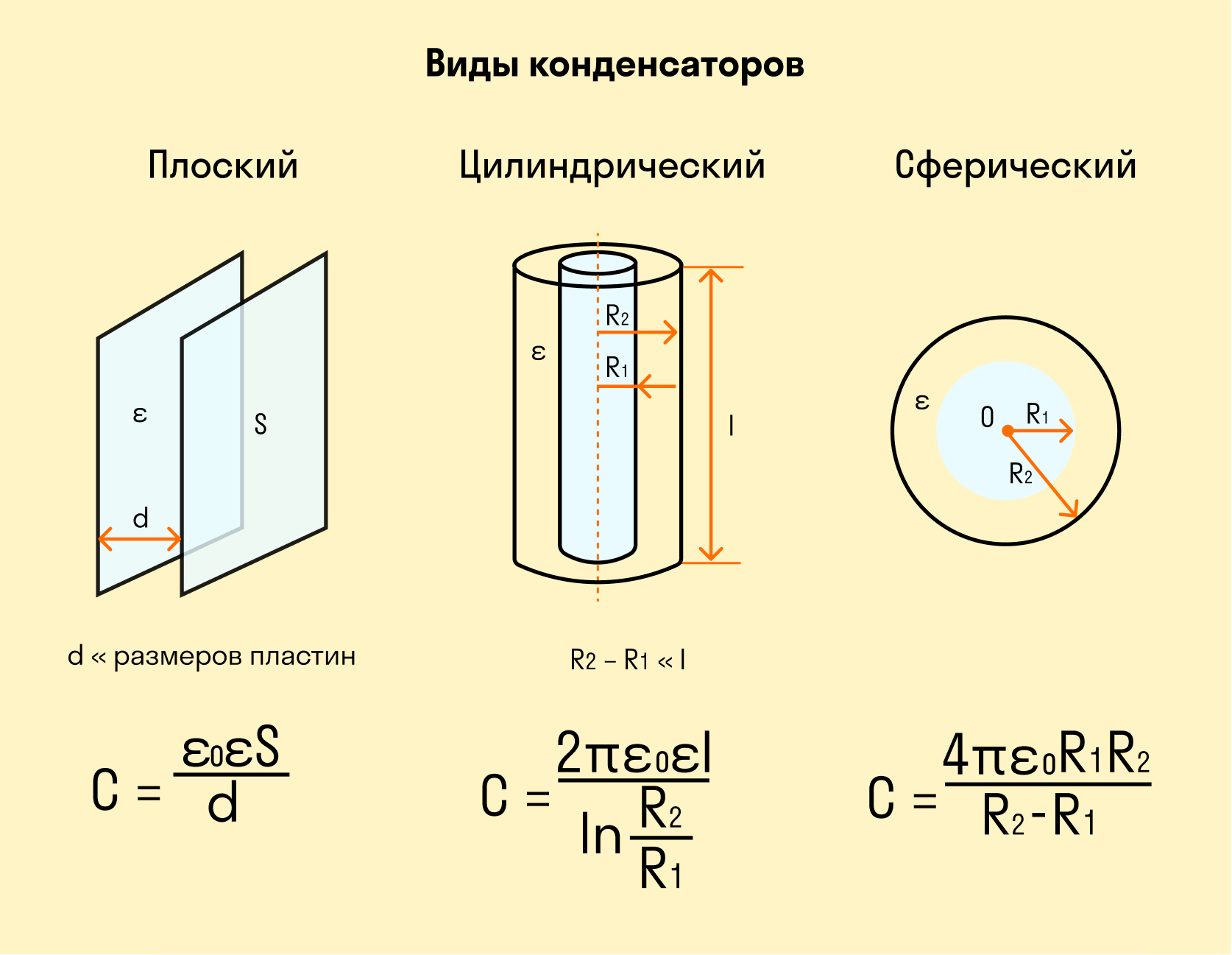
Выделяют три большие группы: плоские, сферические, цилиндрические. Чтобы найти емкость, необходимо обратиться к определению напряжения конденсатора с известными значениями зарядов на обкладках.
Плоский конденсатор
Плоский конденсатор – это две противоположно заряженные пластины, которые разделены тонким слоем диэлектрика, как показано на рисунке 1 .
Формула для расчета электроемкости записывается как
C = ε ε 0 S d , где S является площадью обкладки, d – расстоянием между ними, ε — диэлектрической проницаемостью вещества. Меньшее значение d способствует большему совпадению расчетной емкости конденсатора с реальной.
При известной электроемкости конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равняется d i , вычисление диэлектрической проницаемости этого слоя ε i выполняется, исходя из формулы:
C = ε 0 S d 1 ε 1 + d 2 ε 2 + . . . + d N ε N .
Сферический конденсатор
Когда проводник имеет форму шара или сферы, тогда внешняя замкнутая оболочка является концентрической сферой, это означает, что конденсатор сферический.
Он состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком, как показано на рисунке 2 . Емкость рассчитывается по формуле:
C = 4 π ε ε 0 R 1 R 2 R 2 — R 1 , где R 1 и R 2 являются радиусами обкладок.
Цилиндрический конденсатор
Емкость цилиндрического конденсатора равняется:
C = 2 πεε 0 l ln R 2 R 1 , где l — высота цилиндров, R 1 и R 2 — радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке 3 .
Важной характеристикой конденсаторов считается пробивное напряжение — напряжение, при котором происходит электрический разряд через слой диэлектрика.
U m a x находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.
Электроемкость плоского конденсатора. Формулы
Кроме отдельных конденсаторов используются их соединения. Наличие параллельного соединения конденсаторов применяют для увеличения его емкости. Тогда поиск результирующей емкости соединения сводится к записи суммы C i , где C i — это емкость конденсатора с номером i :
При последовательном соединении конденсаторов суммарная емкость соединения всегда будет по значению меньше, чем минимальная любого конденсатора, входящего в систему. Для расчета результирующей емкости следует сложить величины, обратные к емкостям отдельных конденсаторов:
Произвести вычисление емкости плоского конденсатора при известной площади обкладок
1 с м 2 с расстоянием между ними 1 м м . Пространство между обкладками находится в вакууме.
Решение
Чтобы рассчитать электроемкость конденсатора, применяется формула:
ε = 1 , ε 0 = 8 , 85 · 10 — 12 Ф м ; S = 1 с м 2 = 10 — 4 м 2 ; d = 1 м м = 10 — 3 м .
Подставим числовые выражения и вычислим:
C = 8 , 85 · 10 — 12 · 10 — 4 10 — 3 = 8 , 85 · 10 — 13 ( Ф ) .
Ответ: C ≈ 0 , 9 п Ф .
Найти напряженность электростатического поля у сферического конденсатора на расстоянии x = 1 с м = 10 — 2 м от поверхности внутренней обкладки при внутреннем радиусе обкладки, равном R 1 = 1 с м = 10 — 2 м , внешнем – R 2 = 3 с м = 3 · 10 — 2 м . Значение напряжения — 10 3 В .
Решение
Производящая заряженная сфера создает напряженность поля. Его значение вычисляется по формуле:
E = 1 4 π ε ε 0 q r 2 , где q обозначают заряд внутренней сферы, r = R 1 + x — расстояние от центра сферы.
Нахождение заряда предполагает применение определения емкости конденсатора С:
Для сферического конденсатора предусмотрена формула вида
C = 4 π ε ε 0 R 1 R 2 R 2 — R 1 с радиусами обкладок R 1 и R 2 .
Производим подстановку выражений для получения искомой напряженности:
E = 1 4 πεε 0 U ( x + R 1 ) 2 4 πεε 0 R 1 R 2 R 2 — R 1 = U ( x + R 1 ) 2 R 1 R 2 R 2 — R 1 .
Данные представлены в системе С И , поэтому достаточно заменить буквы числовыми выражениями:
E = 10 3 ( 1 + 1 ) 2 · 10 — 4 · 10 — 2 · 3 · 10 — 2 3 · 10 — 2 — 10 — 2 = 3 · 10 — 1 8 · 10 — 6 = 3 , 45 · 10 4 В м .
Электроемкость конденсатора
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Электроемкость проводников
Проводники умеют не только проводить через себя электрический ток, но и накапливать заряд. Эта способность характеризуется таким параметром, как электроемкость.
Электроемкость
C = q/φ
С — электроемкость [Ф]
q — электрический заряд [Кл]
φ — потенциал [В]
Особенность этой величины в том, что она зависит от формы проводника. Для каждого вида проводников есть своя формула расчета электроемкости. Самая популярная — формула электроемкости шара.
Электроемкость шара
C = 4πεεr
С — электроемкость [Ф]
ε — относительная диэлектрическая проницаемость среды [-]
ε — электрическая постоянная
ε = 8,85 × 10 -12 Ф/м
r — радиус шара [м]
Конденсаторы
Способность накапливать заряд — полезная штука, поэтому люди придумали конденсаторы. Это такие устройства, которые помогают применять электрическую емкость проводников в практических целях.
Конденсатор состоит из двух проводящих пластин (обкладок), разделенных диэлектриком. Между проводящими пластинами образуется электрическое поле, все силовые линии которого идут от одной обкладки к другой.
Когда заряд накапливается на обкладках, происходит процесс под названием зарядка конденсатора. Заряды на разных обкладках равны по величине и противоположны по знаку.
Электроемкость конденсатора измеряется отношением заряда на одной из обкладок к разности потенциалов между обкладками:
Электроемкость конденсатора
C = q/U
С — электроемкость [Ф]
q — электрический заряд [Кл]
U — напряжение (разность потенциалов) [В]
По закону сохранения заряда, если обкладки заряженного конденсатора соединить проводником, то заряды нейтрализуются, переходя с одной обкладки на другую. Так происходит разрядка конденсатора.
Любой конденсатор имеет предел напряжения. Если оно окажется слишком большим, то случится пробой диэлектрика, то есть разрядка произойдет прямо через диэлектрик. Такой конденсатор больше работать не будет.
Виды конденсаторов
Энергия конденсатора
У конденсатора, как и у любой системы заряженных тел, есть энергия. Чтобы зарядить конденсатор, необходимо совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии эта работа будет как раз равна энергии конденсатора.
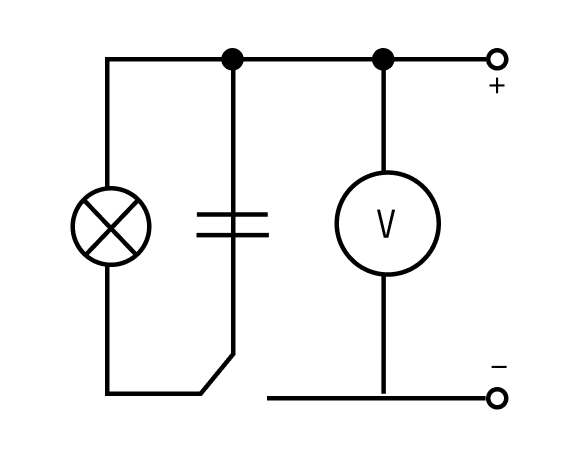
Доказать, что заряженный конденсатор обладает энергией, несложно. Для этого понадобится электрическая цепь, содержащая в себе лампу накаливания и конденсатор. При разрядке конденсатора вспыхнет лампа — это будет означать, что энергия конденсатора превратилась в тепло и энергию света.
Чтобы вывести формулу энергии плоского конденсатора, нам понадобится формула энергии электростатического поля.
Энергия электростатического поля
Wp = qEd
Wp — энергия электростатического поля [Дж]
q — электрический заряд [Кл]
E — напряженность электрического поля [В/м]
d — расстояние от заряда [м]
В случае с конденсатором d будет представлять собой расстояние между пластинами.
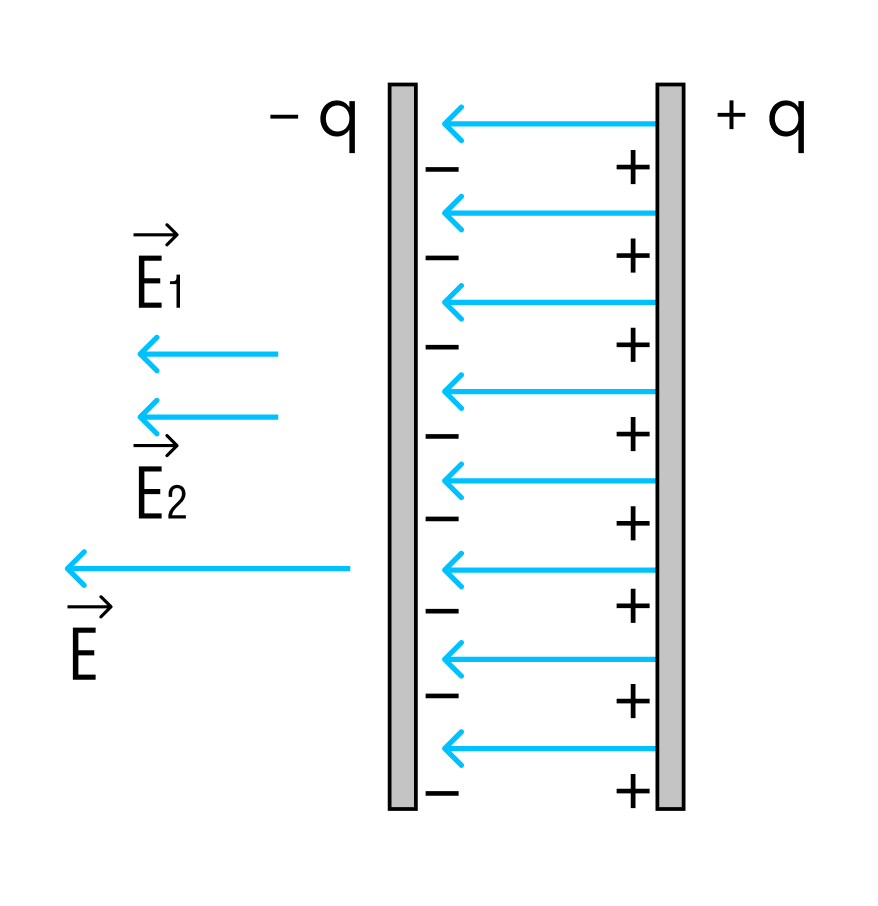
Заряд на пластинах конденсатора равен по модулю, поэтому можно рассматривать напряженность поля, создаваемую только одной из пластин.
Напряженность поля одной пластины равна Е/2, где Е — напряженность поля в конденсаторе.
В однородном поле одной пластины находится заряд q, распределенный по поверхности другой пластины.
Тогда энергия конденсатора равна:
Wp = qEd/2
Разность потенциалов между обкладками конденсатора можно представить, как произведение напряженности на расстояние:
U = Ed
Wp = qU/2
Эта энергия равна работе, которую совершит электрическое поле при сближении пластин.
Заменив в формуле разность потенциалов или заряд с помощью выражения для электроемкости конденсатора C = q/U, получим три различных формулы энергии конденсатора:
Энергия конденсатора
Wp = qU/2
Wp — энергия электростатического поля [Дж]
q — электрический заряд [Кл]
U — напряжение на конденсаторе [В]
Энергия конденсатора
Wp = q 2 /2C
Wp — энергия электростатического поля [Дж]
q — электрический заряд [Кл]
C — электроемкость конденсатора [Ф]
Энергия конденсатора
Wp = CU 2 /2
Wp — энергия электростатического поля [Дж]
C — электроемкость конденсатора [Ф]
U — напряжение на конденсаторе [В]
Эти формулы справедливы для любого конденсатора.
Применение конденсаторов
Конденсатор есть в каждом современном устройстве. Без него не будет работать ни один прибор. Разберем два самых наглядных примера.
Пример раз — вспышка
Без конденсатора вспышка в фотоаппарате работала бы не так, как мы привыкли, а с большими задержками, и к тому же быстро разряжала бы аккумулятор. Конденсатор в этом случае работает как батарейка. Он накапливает заряд от аккумулятора и хранит его до востребования. Когда нам нужна вспышка, конденсатор разряжается, чтобы она сработала и вылетела птичка.
Пример два — тачскрин
Тачскрин на телефоне работает по принципу, схожему с конденсатором. В самом смартфоне, конечно, тоже есть множество конденсаторов, но этот принцип куда интереснее.
Дело в том, что тело человека тоже умеет проводить электричество — у него даже есть сопротивление и электроемкость. Так что можно считать человеческий палец пластиной конденсатора — тело же проводник, почему бы и нет. Но если поднести палец к металлической пластине, получится плохой конденсатор.
В экран телефона встроена матрица из микроскопических пластинок. Когда мы подносим палец к одной из них, получается своего рода конденсатор. Когда перемещаем палец ближе к другой пластинке — еще один конденсатор. Телефон постоянно проверяет пластинки, и если обнаруживает, что у какой-то из них внезапно изменилась электроемкость, значит, рядом есть палец. Координаты пластинки с изменившейся электроемкостью передаются операционной системе телефона, а она уже решает, что с этими координатами делать.
Кстати, то же самое можно проделать, если взять обычную сосиску и поводить ей по экрану смартфона. Тачскрин будет реагировать на все контакты, как реагирует на человеческий палец.
Это не единственный вариант реализации тачскрина, но один из лучших на сегодняшний день. В айфоне используется именно он.
Изучать физику на примерах из реальной жизни может быть очень даже интересно. Попробуйте и убедитесь сами на классическом курсе по физике для 10 класса.
Конденсаторы, свойства конденсатора, обозначение конденсаторов на схемах, основные параметры
Что такое конденсатор? Конденсатор это система из двух и более электродов (обычно в форме пластин, называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок конденсатора. Такая система обладает взаимной ёмкостью и способна сохранять электрический заряд.ТОесть из рисунка видно что это две параллельные металические пластины разделённые каким то материалом (диэлектриком- это вещество которое не проводит электрический ток)
Немного из истоиии изобретения конденсатора
В 1745 году в Лейдене немецкий физик Эвальд Юрген фон Клейст и голландский физик Питер ван Мушенбрук создали первый конденсатор — .
Лейденская банка — первый электрический конденсатор, изобретённый голландскими учёными Мушенбреком и его учеником Кюнеусом в 1745 в Лейдене. Параллельно и независимо от них сходный аппарат, под названием изобрёл немецкий учёный Клейст. Лейденская банка представляла собой закупоренную наполненную водой стеклянную банку, оклеенную внутри и снаружи фольгой. Сквозь крышку в банку был воткнут металлический стержень. Лейденская банка позволяла накапливать и хранить сравнительно большие заряды, порядка микрокулона. Изобретение лейденской банки стимулировало изучение электричества, в частности скорости его распространения и электропроводящих свойств некоторых материалов. Выяснилось, что металлы и вода лучшие проводники электричества. Благодаря Лейденской банке удалось впервые искусственным путем получить электрическую искру.
Свойства конденсатора
Конденсатор в цепи постоянного тока не проводит ток, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора. В терминах метода комплексных амплитуд конденсатор обладает комплексным импедансом
При изменении частоты изменяются диэлектрическая проницаемость диэлектрика и степень влияния паразитных параметров — собственной индуктивности и сопротивления потерь. На высоких частотах любой конденсатор можно рассматривать как последовательный колебательный контур, образуемый ёмкостью , собственной индуктивностью и сопротивлением потерь . Резонансная частота конденсатора равна:
Обозначение конденсаторов на схемах
На электрических принципиальных схемах номинальная ёмкость конденсаторов обычно указывается в микрофарадах или пикофарадах (1 мкФ = 106 пФ). При ёмкости не более 0,01 мкФ, ёмкость конденсатора указывают в пикофарадах, при этом допустимо не указывать единицу измерения, т.е. постфикс опускают. При обозначении номинала ёмкости в других единицах указывают единицу измерения (пикоФарад). Для электролитических конденсаторов, а также для высоковольтных конденсаторов на схемах, после обозначения номинала ёмкости, указывают их максимальное рабочее напряжение в вольтах(В) или киловольтах(кВ). Например так: . Для переменных конденсаторов указывают диапазон изменения ёмкости, например так: .
Характеристики конденсаторов
Основные параметры конденсаторов
Ёмкость конденсаторов
Основной характеристикой конденсатора является его электрическая ёмкость (точнее номинальная ёмкость), которая определяет его заряд в зависимости от напряжения на обкладках (q = CU). Типичные значения ёмкости конденсаторов составляют от единиц пикофарад до сотен микрофарад. Однако существуют конденсаторы с ёмкостью до десятков фарад.
Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.
Если у всех параллельно соединённых конденсаторов расстояние между обкладками и свойства диэлектрика одинаковы, то эти конденсаторы можно представить как один большой конденсатор, разделённый на фрагменты меньшй площади. При последовательном соединении конденсаторов заряды всех конденсаторов одинаковы. Общая ёмкость батареи последовательно соединённых конденсаторов равна
Эта ёмкость всегда меньше минимальной ёмкости конденсатора, входящего в батарею. Однако при последовательном соединении уменьшается возможность пробоя конденсаторов, так как на каждый конденсатор приходится лишь часть разницы потенциалов источника напряжения. Если площадь обкладок всех конденсаторов, соединённых последовательно, одинакова, то эти конденсаторы можно представить в виде одного большого конденсатора, между обкладками которого находится стопка из пластин диэлектрика всех составляющих его конденсаторов.
Удельная ёмкость конденсаторов
Конденсаторы также характеризуются удельной ёмкостью — отношением ёмкости к объёму (или массе) диэлектрика. Максимальное значение удельной ёмкости достигается при минимальной толщине диэлектрика, однако при этом уменьшается его напряжение пробоя.
Номинальное напряжение конденсаторов
Другой, не менее важной характеристикой конденсаторов является номинальное напряжение — значение напряжения, обозначенное на конденсаторе, при котором он может работать в заданных условиях в течение срока службы с сохранением параметров в допустимых пределах. Номинальное напряжение зависит от конструкции конденсатора и свойств применяемых материалов. При эксплуатации напряжение на конденсаторе не должно превышать номинального. Для многих типов конденсаторов с увеличением температуры допустимое напряжение снижается.
Номинальное напряжение конденсаторов
Другой, не менее важной характеристикой конденсаторов является номинальное напряжение — значение напряжения, обозначенное на конденсаторе, при котором он может работать в заданных условиях в течение срока службы с сохранением параметров в допустимых пределах. Номинальное напряжение зависит от конструкции конденсатора и свойств применяемых материалов. При эксплуатации напряжение на конденсаторе не должно превышать номинального. Для многих типов конденсаторов с увеличением температуры допустимое напряжение снижается.
Полярность конденсаторов
Многие конденсаторы с оксидным диэлектриком (электролитические) функционируют только при корректной полярности напряжения из-за химических особенностей взаимодействия электролита с диэлектриком. При обратной полярности напряжения электролитические конденсаторы обычно выходят из строя из-за химического разрушения диэлектрика с последующим увеличением тока, вскипанием электролита внутри и, как следствие, с вероятностью взрыва корпуса. Взрывы электролитических конденсаторов — довольно распространённое явление. Основной причиной взрывов является перегрев конденсатора, вызываемый в большинстве случаев утечкой или повышением эквивалентного последовательного сопротивления вследствие старения (актуально для импульсных устройств). Для уменьшения повреждений других деталей и травматизма персонала в современных конденсаторах большой ёмкости устанавливают клапан или выполняют насечку на корпусе (часто можно заметить её в форме буквы X, K или Т на торце). При повышении внутреннего давления открывается клапан или корпус разрушается по насечке, испарившийся электролит выходит в виде едкого газа, и давление спадает без взрыва и осколков.
Паразитные параметры конденсаторов
Реальные конденсаторы, помимо ёмкости, обладают также собственными сопротивлением и индуктивностью. С высокой степенью точности, эквивалентную схему реального конденсатора можно представить следующим образом:
Электрическое сопротивление изоляции конденсатора — r
Эквивалентное последовательное сопротивление — R
Эквивалентное последовательное сопротивление (ЭПС, англ. ESR) обусловлено главным образом электрическим сопротивлением материала обкладок и выводов конденсатора и контакта(-ов) между ними, а также потерями в диэлектрике. Обычно ЭПС возрастает с увеличением частоты тока, протекающего через конденсатор. В большинстве случаев этим параметром можно пренебречь, но иногда (напр., в случае использования электролитических конденсаторов в фильтрах импульсных блоков питания) достаточно малое его значение может быть жизненно важным для надёжности устройства (см., напр., Capacitor plague(англ.)).
Эквивалентная последовательная индуктивность — L
Тангенс угла потерь
Температурный коэффициент ёмкости (ТКЕ) конденсаторов
где ?T — увеличение температуры в °C или °К относительно нормальных условий, при которых специфицировано значение ёмкости. TKE применяется для характеристики конденсаторов со значительной линейной зависимостью ёмкости от температуры. Однако ТКЕ определяется не для всех типов конденсаторов. Для характеристики конденсаторов с выраженной нелинейной зависимостью обычно указывают предельные величины отклонений от номинала в рабочем диапазоне температур.
Диэлектрическое поглощение конденсаторов
Если заряженный конденсатор быстро разрядить до нулевого напряжения путём подключения низкоомной нагрузки, а затем снять нагрузку и наблюдать за напряжением на выводах конденсатора, то мы увидим, что напряжение медленно повышается. Это явление получило название диэлектрическое поглощение или адсорбция электрического заряда. Конденсатор ведёт себя так, словно параллельно ему подключено множество последовательных RC-цепочек с различной постоянной времени. Интенсивность проявления этого эффекта зависит в основном от свойств диэлектрика конденсатора. Наименьшим диэлектрическим поглощением обладают конденсаторы с тефлоновым (фторопластовым) диэлектриком. Подобный эффект можно наблюдать и на большинстве электролитических конденсаторов, но в них он является следствием химических реакций между электролитом и обкладками.
Классификация конденсаторов(типы конденсаторов)
Краткое обозначение!Типы конденсаторов:
БМ — бумажный малогабаритный
БМТ — бумажный малогабаритный теплостойкий
КД — керамический дисковый
КЛС — керамический литой секционный
КМ — керамический монолитный
КПК-М — подстроечный керамический малогабаритный
КСО — слюдянной опресованный
КТ — керамический трубчатый
МБГ — металлобумажный герметизированный
МБГО — металлобумажный герметизированный однослойный
МБГТ — металлобумажный герметизированный теплостойкий
МБГЧ — металлобумажный герметизированный однослойный
МБМ — металлобумажный малогабаритный
ПМ — полистироловый малогабаритный
ПО — пленочный открытый
ПСО — пленочный стирофлексный открытый