Классификация кривых поверхностей
Все многообразие поверхностей можно отнести к двум классам:
I класс составляют поверхности, образующие которых кривые линии (нелинейчатые);
II класс – поверхности, образованные прямой линией (линейчатые).
При отнесении поверхностей к классам I или II во внимание принималась геометрическая часть определителя – вид линии, образующей поверхность.
Условия алгоритмической части определителя, характеризующие закон движения образующей, позволяют выделить из этих двух классов три подкласса.
1 подкласс содержит поверхности, образованные поступательным перемещением образующей линии.
Такие поверхности называют поверхностями параллельного переноса, определитель Ф(g; d)(рис.8).
| а) нелинейчатые; | б) линейчатые; |
Рис. 8
Линейчатые поверхности с одной криволинейной направляющей называются торсами.
2 подкласс составляют поверхности, образованные вращением образующей линии(рис.9).
| а) нелинейчатые; | б) линейчатые; |
Рис. 9
3 подкласс включает поверхности, образованные винтовым перемещением образующей(рис.10).
| а) нелинейчатые; | б) линейчатые; |
Рис. 10
Поверхности подклассов1,2 и 3 имеют одинаковую геометрическую часть определителя. В зависимости от вида образующей (кривая или прямая) поверхности параллельного переноса, вращения, винтовые могут быть отнесены как к первому (g – кривая), так и ко второму (g – прямая) классам.
Линейчатые поверхности
Линейчатая поверхность в общем случае однозначно определяются тремя направляющими линиями,
Классификация линейчатых поверхностей в зависимости от вида определителя, содержащего информацию о числе направляющих, показаны на рисунке 11.
| Линейчатые поверхности | ||
| А. Три направляющие | Б. Две направляющие | В. Одна направляющая |
| Косой цилиндр с тремя направляющими | Образующая составляет постоянный угол с направляющей плоскостью | Поверхность с ребром возврата |
| Дважды косой цилиндр | Косой цилиндроид | Цилиндрическая поверхность |
| Дважды косой коноид | Косой коноид | Коническая поверхность |
| Однополостный гиперболоид | Дважды косая плоскость | Плоскость |
Рис.11. Классификация линейчатых поверхностей
Из рисунка 11видно что все многообразие линейных поверхностей может быть отнесено к трем группам:
группа А – линейчатые поверхности с тремя направляющими;
группа Б – линейчатые поверхности с двумя направляющими;
группа В – линейчатые поверхности с одной направляющей.
Винтовые поверхности
Поверхность называется винтовой, если она получается винтовым перемещением образующей.
В зависимости от формы образующей отдельные виды винтовых поверхностей могут быть отнесены как к классу линейчатых поверхностей, так и к классу нелинейчатых поверхностей.
Выделение этих поверхностей в самостоятельный подкласс связано со стремлением подчеркнуть значение винтовых поверхностей в технике, архитектурно строительной практике и, особенно, в машиностроении. Винтовая поверхность с криволинейной образующей показана на рисунке 10.
Винтовая поверхность с прямолинейной образующей и направляющей винтовой линией показана так же на рисунке 10.
Все точки образующей при винтовом движении описывают винтовые линии, каждая из которых может служить направляющей поверхности. Такие линии называют винтовыми параллелями. Все винтовые параллели имеют одинаковый шаг, называемый шагом винтовой поверхности.
Характерной особенностью для винтовых поверхностей с постоянным шагом является постоянство угла наклона прямолинейной образующей к направляющей плоскости, за которую принята плоскость, перпендикулярная оси винтовой поверхности.
Винтовая линия постоянного шага, построенная на поверхности прямого кругового цилиндра, называется гелисой. Поэтому линейчатые винтовые поверхности, направляющая которых – гелиса, называются геликоидами. В зависимости от угла наклона образующей к оси геликоида бывают прямыми, если этот угол равен 90º и косыми (наклонными), если угол произвольный, отличный от 0º и 90º.
В свою очередь, прямые и косые геликоиды подразделяются на закрытые и открытые. Признаком такого деления служит взаимное расположение оси геликоида и его образующей. Если образующая и ось пересекаются, то геликоид называют закрытым, если скрещиваются – открытым.
Следует отметить одно важное свойство винтовых поверхностей, состоящее в том что эти поверхности, так же как и поверхности вращения, могут сдвигаться, т.е., совершая винтовое перемещение, поверхность скользит вдоль самой себя. Это свойство обеспечивает винтовым поверхностям широкое применение в технике. Винты, шнеки, сверла, пружины, поверхности лопаток вентиляторов, рабочие органы сельскохозяйственных машин, конструкции винтовых лестниц – вот далеко не полный перечень технического использования винтовых поверхностей.
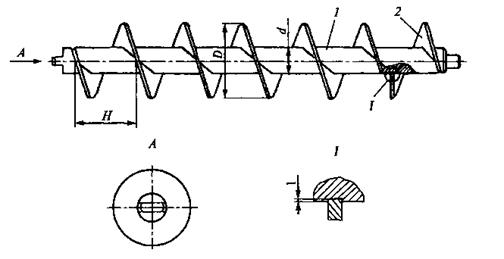
Практическое применение винтовые поверхности находят в курсовом проектировании по дисциплинам: «Подъемно-транспортные машины», «Механизация животноводства», «Сельскохозяйственные машины» и другим, в дипломном проектировании винтовых транспортеров (шнеков) для перемещения зерна, мелкокусковых материалов и др., шнековых прессов для цехов кормопроизводства, маслоцехов, соковыжимных цехов. На рисунках 154, 155 даны примеры шнеков прямоугольного профиля со сплошным и полым валом.
Рис. 12. Шнек со сплошным валом: 1 — вал; 2 — виток
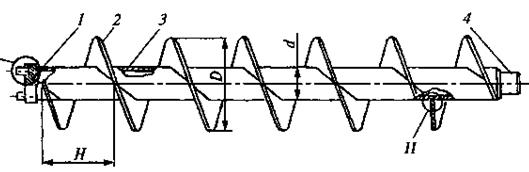
Рис. 13. Шнек с полым валом:
1 — опорная цапфа; 2 — виток; 3 — полый вал; 4 — ведущая цапфа;
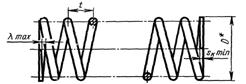
На рисунках 14а, 14б даны примеры пружин сжатия, растяжения.
Рис. 14а. Пружина сжатия с предварительно обработанными концами заготовки
Рис. 14б. Пружина растяжения
Поверхности вращения
Поверхностью вращения общего вида называют поверхность, которая образуется произвольной прямой или кривой (плоской или пространственной) при ее вращении вокруг неподвижной оси.
Каждая точка образующей при вращении вокруг оси описывает окружность с центром на оси вращения. Эти окружности называют параллелями. Наибольшую параллель называют экватором.
Плоскости, проходящие через ось поверхности вращения, называют меридиональными, а линии, по которым они пересекают поверхность, – меридианами. Меридиональную плоскость, параллельную плоскости проекций π2, принято называть главноймеридиональной плоскостью, а линию пересечения с поверхностью вращения – главным меридианом.
При задании поверхности вращения на чертеже обычно указывают проекции ее оси, главного меридиана и экватора.
В технике, в частности в машиностроении, поверхности вращения находят широкое применение. Это объясняется распространенностью вращательного движения на станках.
Особенно распространены поверхности, имеющие в меридиональном сечении кривую второго порядка или две прямые, на которые распадается эта кривая.
Некоторые поверхности вращения представляют собой частные случаи поверхностей, в качестве образующей которых является окружность. В зависимости от взаимного расположения окружности (или ее дуги) и оси вращения можно получить различные поверхности:
1) тор(рис. 15 – 18);
тором называется поверхность, которая может быть получена при вращении окружности вокруг оси, не проходящей через ее центр.
В зависимости от соотношения величин R – радиуса образующей окружности и расстояния t от центра окружности до оси вращения поверхности тора подразделяют:
а) открытый тор (или кольцо) при R Рис. 15 б) замкнутый тор, R = t(рис.158); Рис.16 в) самопересекающийся тор, R>t(рис.159); Рис.17 2)цилиндр вращения(рис.18); Рис.18 3) конус вращения(рис.19); Рис.19 Для цилиндра и конуса вращения меридианы являются прямыми линиями – в первом случае параллельными оси и равноудаленными от нее, во втором случае пересекающими ось в одной и той же точке, под одним и тем же углом к оси. Меридиан цилиндра на рисунке 160 – прямоугольник, а конуса на рисунке 161 – треугольник. 4) сфера(рис.20); Рис. 20 Сфера образуется в том случае, когда центр окружности принадлежит оси вращения. Сферу можно рассматривать как частный случай тора, у которого t=0. 5) гиперболоид вращения (рис. 21); Для гиперболоида вращения меридианом является гипербола, причем если осью вращения служит действительная ось гиперболы, то образуется двуполостный гиперболоид вращения; если же вращать гиперболу вокруг её мнимой оси, то однополостный. Однополостный гиперболоид вращения может быть образован также вращением прямой линии в случае, если образующая и ось вращения – скрещивающиеся прямые. На рисунке 21 показан однополостный гиперболоид вращения, образованный вращением прямой АВ вокруг указанной оси и ограниченный двумя параллелями. На однополостном гиперболоиде вращения можно нанести прямолинейные образующие в двух направлениях, например так, как показано на рисунке 21, и с наклоном в обратную сторону, под тем же углом к оси. Кроме прямых (пар) на этой поверхности могут быть ещё гиперболы, параболы, эллипсы и окружности. Рис. 21 Для параболоида вращения меридианом является парабола, ось которой служит осью поверхности. Для эллипсоида вращения меридианом является эллипс. Поверхность может быть образована вращением эллипса вокруг его большой оси («вытянутый» эллипсоид вращения) или вокруг его малой оси («сжатый» эллипсоид вращения)(рис. 22). а) «вытянутый» эллипсоид б) «сжатый» эллипсоид Рис. 22 Особенно часто встречаются в курсовом и дипломном проектировании валы, оси, шкивы, крышки, шестерни и т.д. Линейчатые поверхности — поверхности, которые образуются с помощью прямой линии. Нелинейчатые поверхности — поверхности, которые образуются с помощью кривой линии. Развертывающиеся поверхности — поверхности, которые после разреза их по образующей могут быть совмещены с плоскостью без наличия разрывов и складок. Неразвертывающиеся поверхности — поверхности, которые не могут быть совмещены с плоскостью без наличия разрывов и складок. Поверхности с постоянной образующей — поверхности, образующая которых не изменяет своей формы в процессе образования поверхности. Поверхности с переменной образующей — поверхности, образующая которых изменяется в процессе образования поверхности. Линейчатые развертываемые поверхности: 1. Конические поверхности задаются движением прямой линии l, проходящей через неподвижную точку М, по некоторой направляющей кривой линии а. (рис 128) 2. Цилиндрические поверхности задаются движением прямой, параллельной некоторому направлению, по заданной направляющей кривой. (рис 129) 3. Линейчатые неразвертываемые поверхности: 1) Цилиндроидобразован движением прямой, параллельной заданной плоскости параллелизма α, по двум пространственным кривым a и b. 2) Коноид образован движением прямой по одной прямолинейной направляющей n, по другой криволинейной направляющей m, оставаясь параллельной некоторой плоскости параллелизма α || π1. 3) Гиперболический параболоид, или косая плоскость, задается двумя скрещивающимися прямыми направляющими АВ, CD и плоскостью параллелизма α(απ1). 4) Однополостный гиперболоид образуется движением прямолинейной образующей l по трем прямолинейным скрещивающимся направляющим а, b, c. 5) Косой цилиндр с тремя направляющими образуется движением прямолинейной образующей по трем направляющим, одна из которых обязательно кривая. Нелинейчатые неразвертываемые поверхности: 1) Эллипсоид трехосный образован движением переменного эллипса вдоль одной из трех его осей Х, Y, Z . Образующие эллипсы подобны. 2) Эллиптический параболоид образуется движением деформирующегося эллипса по двум направляющим параболам m и n 3) Двуполостный гиперболоид образуется движением изменяющегося эллипса по направляющей гиперболе вдоль действительной оси. Точка принадлежит поверхности, если она расположена на линии, принадлежащей поверхности. На поверхностях вращения в качестве таких линий удобно использовать параллели. Если на поверхности вращения (рис. 8.9) дана проекция М2, то для нахождения параллели, которой принадлежит точка М, проводим через М фронтально-проецирующую плоскость s (М2 ϵ s), такую что s ⊥ m. Тогда линия пересечения кривой поверхности с плоскостью s и даст искомую параллель. Радиус параллели равен расстоянию от оси вращения m1 до точки поверхности 11. Этим радиусом проводим окружность с центром в точке m1 (горизонтальной проекции оси вращения) и получаем горизонтальную проекцию параллели. На ней находим горизонтальные проекции точки М: М1 — на видимой стороне кривой поверхности, а М’1 — на невидимой. Линия принадлежит поверхности, если все ее точки принадлежат этой поверхности. Исключение составляет случай, когда линия представлена прямой, а поверхность — плоскостью. В этом случае для принадлежности прямой плоскости достаточно, чтобы хотя бы две точки ее принадлежали этой поверхности. Если линия не принадлежит поверхности, то они пересекаются. Простейшим случаем является пересечение с поверхностью прямой линии. Задача решается путем заключения данной линии в какую-либо проецирующую плоскость и построением натуральной величины сечения, из которого легко определить точку входа и выхода прямой. Поверхностью называют множество последовательных положений линий, перемещающихся в пространстве. Эта линия может быть прямой или кривой и называется образующей поверхности. Если образующая кривая, она может иметь постоянный или переменный вид. Перемещается образующая по направляющим, представляющим собой линии иного направления, чем образующие. Направляющие линии задают закон перемещения образующим. При перемещении образующей по направляющим создается каркас поверхности (рис. 84), представляющий собой совокупность нескольких последовательных положений образующих и направляющих. Рассматривая каркас, можно убедиться, что образующие l и направляющие т можно поменять местами, но при этом по верхность получается одна и та же. Любую поверхность можно получить различными способами. Так, прямой круговой цилиндр (рис. 85) можно создать вращением образующей l вокруг оси г, ей параллельной. Тот же цилиндр образуется перемещением окружности т с центром в точке О, скользящим по оси i. Любая кривая k, лежащая на поверхности цилиндра, образует эту поверхность при своем вращении вокруг оси /’. На практике из всех возможных способов образования поверхности выбирают наиболее простой. В зависимости от формы образующей все поверхности можно разделить на линейчатые, у которых образующая прямая линия, и нелинейчатые, у которых образующая кривая линия. В линейчатых поверхностях выделяют поверхности развертывающиеся, совмещаемые всеми своими точками с плоскостью без разрывов и складок, и неразвертывающиеся, которые нельзя совместить с плоскостью без разрывов и складок. К развертывающимся поверхностям относятся поверхности всех многогранников, цилиндрические, конические и торсовые поверхности. Все остальные поверхности — неразвертывающиеся. Нелинейчатые поверхности могут быть с образующей постоянной формы (поверхности вращения и трубчатые поверхности) и с образующей переменной формы (каналовые и каркасные поверхности). Для задания поверхностей выбирают такую совокупность независимых геометрических условий, которая однозначно определяет данную поверхность в пространстве. Эта совокупность условий называется определителем поверхности. Определитель состоит из двух частей: геометрической, в которую входят основные геометрические элементы и соотношения между ними, и алгоритмической, содержащей последовательность и характер операций перехода от основных постоянных элементов и величин к переменным элементам поверхности, т. е. закон построения отдельных точек и линий данной поверхности. Поверхность на комплексном чертеже задается проекциями геометрической части ее определителя с указанием способа построения ее образующих. На чертеже поверхности для любой точки пространства однозначно решается вопрос о принадлежности ее данной поверхности. Графическое задание элементов определителя поверхности обеспечивает обратимость чертежа, но не делает его наглядным. Для наглядности прибегают к построению проекций достаточно плотного каркаса образующих и к построению очерковых линий поверхности (рис. 86). При проецировании поверхности Q на плоскость проекций проецирующие лучи прикасаются к этой поверхности в точках, образующих на ней некоторую линию l, которая называется контурной линией. Проекция контурной линии называется очерком поверхности. На комплексном чертеже любая поверхность имеет: на П1— горизонтальный очерк, на П2 — фронтальный очерк, на П3 — профильный очерк поверхности. Очерк включает в себя, кроме проекций линии контура, также проекции линий обреза. Из существенного множества поверхностей в курсе инженерной графики будут рассмотрены все развертывающиеся поверхности, к которым относятся гранные, конические, цилиндрические, торсовые поверхности, некоторые поверхности вращения и винтовые. Простейшей поверхностью, широко используемой в инженерной графике, является плоскость, представляющая собой поверхность, образованную перемещением прямолинейной образующей (рис. 87) по двум параллельным или пересекающимся прямым m1и m2. В начертательной геометрии поверхность рассматривают как множество последовательных положений движущейся линии или другой поверхности в пространстве. Линию, перемещающуюся в пространстве и образующую поверхность, называют образующей. Образующие могут быть прямыми и кривыми. Образующие поверхность кривые могут быть постоянными и переменными, например закономерно изменяющимися. Одна и та же поверхность в ряде случаев может рассматриваться как образованная движениями различных образующих. Например, круговой цилиндр может быть образован: во-первых, вращением прямой относительно неподвижной оси, параллельной образующей; во-вторых, движением окружности, центр которой перемещается по прямой, перпендикулярной плоскости окружности; в-третьих, прямолинейным движением сферы. При изображении поверхности на чертеже показывают лишь некоторые из множества положений образующей. На рисунке 8.1 показана поверхность с образующей АВ. При своем движении образующая остается параллельной выбранному направлению MN и одновременно пересекает некоторую кривую линию CDE. Таким образом движение образующей АВ направляется в пространстве линией CDE. Линию или линии, пересечение с которыми является обязательным условием движения образующей при образовании поверхности, называют направляющей или направляющими. На рисунке 8.2 показана проекция поверхности, образованной движением прямой АВ по двум направляющим — прямой 0102 (АВ перпендикулярно 0102) и пространственной кривой FGQ, не пересекающей прямую 0102. Иногда в качестве направляющей используют линию, по которой движется некоторая характерная для образующей точка, но не лежащая на ней, например центр окружности. Из различных форм образующих, направляющих, а также закономерностей образования конкретной поверхности выбирают те, которые являются наиболее простыми и удобными для изображения на чертеже поверхности и решения задач, связанных с нею. Иногда для задания поверхности используют понятие определитель поверхности, под которым подразумевают совокупность независимых условий, однозначно задающих поверхность. В числе условий, входящих в состав определителя, различают геометрическую часть (точки, линии, поверхности) и закон (алгоритм) образования поверхности геометрической частью определителя. Рассмотрим краткую классификацию кривых поверхностей, принятую в начертательной геометрии. Линейчатые развертываемые поверхности. Поверхность, которая может быть образована движением прямой линии, называют линейчатой поверхностью. Если линейчатая поверхность может быть развернута так, что всеми своими точками она совместится с плоскостью без каких-либо повреждений поверхности (разрывов или складок), то ее называют развертываемой. К развертываемым поверхностям относятся только такие линейчатые поверхности, у которых смежные прямолинейные образующие параллельны, или пересекаются между собой, или являются касательными к некоторой заданной пространственной кривой. Все остальные линейчатые и все нелинейчатые поверхности относятся к неразвертываемым поверхностям. Развертываемые поверхности — цилиндрические, конические, с ребром возврата или торсовые. У цилиндрической поверхности образующие всегда параллельны, направляющая — одна кривая линия. Изображение на чертеже ранее показанной в пространстве цилиндрической поверхности (см. рис. 8.1) представлено на рисунке 8.3. Частные случаи — прямой круговой цилиндр, наклонный круговой цилиндр (см. рис. 9.17, направляющая — окружность, плоскость которой расположена под углом к оси цилиндра и с центром на его оси). У конических поверхностей все прямолинейные образующие имеют общую неподвижную точку — вершину, направляющая — одна любая кривая линия. Пример изображения конической поверхности на чертеже — рисунок 8.4, проекции вершины s’, s, направляющей c’d’e’, cde. Частные случаи — прямой круговой конус, наклонный круговой конус (см. рис. 10.10, справа). У поверхностей с ребром возврата или торсовых прямолинейные образующие касательны к одной криволинейной направляющей. Линейчатые неразвертываемые поверхности: цилиндроид, коноид, гиперболический параболоид (косая плоскость). Поверхность, называемая цилиндроидом, образуется при перемещении прямой линии, во всех своих положениях сохраняющей параллельность некоторой заданной плоскости («плоскости параллелизма») и пересекающей две кривые линии (две направляющие). Поверхность, называемая коноидом, образуется при перемещении прямой линии, во всех своих положениях сохраняющей параллельность некоторой плоскости («плоскости параллелизма») и пересекающей две направляющие, одна из которых кривая, а другая прямая линия (рис. 8.5, см. также рис. 8.2). Плоскостью параллелизма на рисунке 8.5 является плоскость Н, направляющие — кривая с проекциями a’g’q’, agq, прямая с проекциями o1‘o2‘, o1o. В частном случае, если криволинейная направляющая — цилиндрическая винтовая линия с осью, совпадающей с прямолинейной направляющей, образуемая поверхность — винтовой коноид, рассматриваемый ниже. Чертеж гиперболического параболоида, называемого косой плоскостью, приведен на рисунке 8 . 6 . Образование этой поверхности можно рассматривать как результат перемещения прямолинейной образующей по двум направляющим — скрещивающимся прямым параллельно некоторой плоскости параллелизма. На рисунке 8.6 плоскость параллелизма — плоскость проекций Н, направляющие — прямые с проекциями т’п’, тп и q’g’, qg. Нелинейчатые поверхности. Их подразделяют на поверхности с постоянной образующей и поверхности с переменной образующей. Поверхности с постоянной образующей в свою очередь подразделяют на поверхности вращения с криволинейной образующей, например сфера, тор, эллипсоид вращения и др. (см. рис. 8.16, 8.13), и на циклические поверхности, например поверхности изогнутых труб постоянного сечения, пружин. Поверхности с переменной образующей подразделяют на поверхности циклические с переменной образующей, топографические поверхности аффинных и подобных линий и т. д. Чертеж поверхности второго порядка — эллипсоида — приведен на рисунке 8.7. Образующая эллипсоида — деформирующийся эллипс, одна из проекций которого, например, d»e»b»f». Две направляющие — два пересекающихся эллипса, плоскости которых ортогональны и одна ось общая, например с проекциями a’e’c’f’ и adcb. Образующая пересекает направляющие в крайних точках своих осей. Плоскость образующего эллипса при перемещении остается параллельной плоскости, образованной двумя пересекающимися осями направляющих эллипсов. Циклические поверхности с переменной образующей имеют образующую — окружность переменного радиуса, направляющую — кривую, по которой перемещается центр образующей, плоскость образующей перпендикулярна к направляющей. Каркасную поверхность задают некоторым множеством линий или точек поверхности. Обычно такие линии — плоские кривые, плоскости которых параллельны между собой. Два пересекающихся семейства линий каркаса образуют сетчатый каркас поверхности. Точки пересечения линий образуют точечный каркас поверхности. Точечный каркас поверхности может быть задан и координатами точек поверхности. Каркасные поверхности широко используют при конструировании корпусов судов, самолетов, автомобилей, баллонов электронно-лучевых трубок (см. форзац).Линейчатые и нелинейчатые поверхности.




§ 45. Образование поверхностей
Общие сведения о поверхностях и их изображении на чертежах