Как правильно измерить угол

Измерение углов. Транспортир. Виды углов

Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения (1 мм, 1 см, 1 м и т.д.). Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения — с градусом, записывают так 1 ° .

Градусная мера угла — это число, которое показывает, сколько раз градус и его части укладываются в данном угле.

Пример:

Градусная мера угла ABC равна . Говорят: «Угол ABC равен 120 градусам». Пишут: .

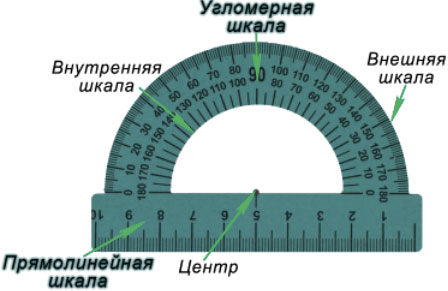
Транспортир — это измерительный инструмент, который используется для измерения и построения углов. Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до .

Для того чтобы измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.

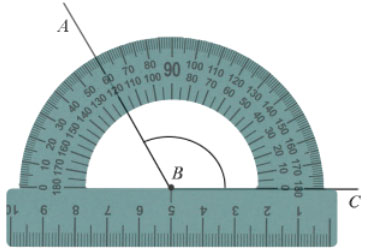
Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).

Вторая сторона при этом, как мы видим, проходит через деление шкалы 120, значит: .

Свойства:

имеют равные градусные меры.
• Меньший угол имеетменьшую градусную меру.
• Развернутый угол равен />.
• Неразвернутый угол меньше />.
• Если лучделит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов, т.е. на рисунке ниже

АОС = АОВ + ВОС.

Виды углов:

1. Острый угол — угол, градусная мера которого меньше 90 ° .

— угол, градусная мера которого равна 90 ° .

1. Тупой угол — угол, градусная мера которого больше 90 °, но меньше 180 ° .

— угол, градусная мера которого равна 180 °.

Биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 90 0 .

АОС — развернутый, ОВ — биссектриса, АОВ = ВОС = 90 0 .

Точный угол 90 градусов с помощью рулетки

При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.

Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.

Теорема Пифагора

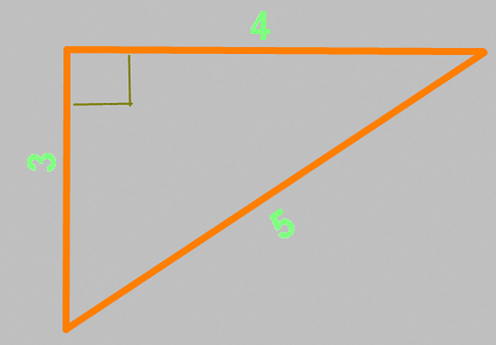
Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:

Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.

Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!

А теперь применим теорему на практике.

Проверка прямого угла

Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.

Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла

Диагональ c

Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.

Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.

Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.

Как разметить прямой угол рулеткой

Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.

Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!

Как разметить острый угол

Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.

Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.

Угол. Измерение углов.

Измерение углов сводится к измерению соответствующих им дуг следующим образом. За единицу углов принимают угол, составляющий 1/90 часть прямого угла. Эту единицу называют угловым градусом.

За единицу дуг одинакового радиуса принимают такую дугу того же радиуса, которая соответствует центральному углу, равному угловому градусу. Такая дуга называется дуговым градусом.

Так как прямому центральному углу соответствует 1/4 окружности, то угловому градусу соответствует 1/90 четверти окружности. Значит, дуговой градус составляет 1/360 целой окружности.

Пусть требуется измерить угол AOB, то есть найти отношение этого угла к угловому градусу MNP.Для этого опишем из вершин углов дуги СD и EF произвольным, но одинаковым радиусом.

Тогда будем иметь:

Левое отношение этой пропорции — число, измеряющее угол AOB в угловых градусах Правое отношение — число, измеряющее дугу СD в дуговых градусах.

Следовательно, эту пропорцию можно выразить так: число, измеряющее угол в угловых градусах, равно числу, измеряющему соответствующую дугу в дуговых градусах.

Для краткости эту фразу выражают обыкновенно так: Угол измеряется соответствующей ему дугой.

Градусы угла или дуги подразделяются на 60 равных частей, называемых минутами (угловыми или дуговыми).

Минуту разделяют на 60 равных частей, называемых секундами (угловыми или дуговыми).

Из сказанного выше следует, что в угле содержится столько угловых градусов, минут и секунд, сколько в соответствующей ему дуге заключается дуговых градусов, минут и секунд.

Если, например, в дуге СD содержится 40 град. 25 мин. и 13,5 секунды (дуговых), то и в угле AOB заключается 40 град. 25 мин. 13,5 сек. (угловых). Это выражают сокращенно так:

обозначая значками (°), (‘), (‘’) соответственно градусы, минуты и секунды.

Так как прямой угол содержит 90°, то :

1. сумма углов всякого треугольника равна 180 °;

2. сумма острых углов прямоугольного треугольника равна 90°;

3. каждый угол равностороннего треугольника равен 60°;

4. сумма углов выпуклого многоугольника, имеющего n сторон, равна 180° (n — 2 ).

Транспортир — это прибор, употребляемый для измерения углов, представляет собой полукруг, дуга которого разделена на 180 градусов.

Чтобы измерить угол AOB, накладывают на него прибор так, чтобы центр полукруга совпал с вершиной угла, а радиусом OM совпал со стороной AO. Тогда число градусов, содержащееся в дуге PN, покажет величину угла AOB. При помощи транспортира можно также начертить угол, содержащий данное число градусов.

Конечно, на таком приборе нет возможности отсчитывать не только секунды, но и минуты. Измерение и построение можно выполнить только приближенно.