Делительная окружность
ДЕЛИТЕЛЬНАЯ ОКРУЖНОСТЬ — окружность зубчатого колеса, по к рой шаг зубьев р= Пи*т, где т стандартный торцевой модуль зубьев(см. рис.). Д. о. в торцевом сечении делит зуб на головку и ножку. К ст. Делительная окружность: d диаметр делительной окружности; р шаг зубьев … Большой энциклопедический политехнический словарь
делительная окружность — standard cirle of cylindrical gear Окружность, которая является базовой для определения размеров зубьев цилиндрического зубчатого колеса. Шифр IFToMM: Раздел: СТРУКТУРА МЕХАНИЗМОВ … Теория механизмов и машин
делительная окружность кабельного изделия — делительная окружность Окружность, проходящая через центры элементов скрутки (проволок, стренг, жил, групп, пучков), образующих повив. [ГОСТ 15845 80] Тематики кабели, провода . Синонимы делительная окружность … Справочник технического переводчика
делительная окружность плоского колеса — Окружность пересечения делительной плоскости плоского колеса дополнительным цилиндром. Примечания: 1. Различают внешнюю, среднюю, внутреннюю и др. делительные окружности плоского колеса, соответствующие внешнему, среднему, внутреннему и др.… … Справочник технического переводчика
Делительная окружность кабельного изделия — 196. Делительная окружность кабельного изделия Делительная окружность Окружность, проходящая через центры элементов скрутки (проволок, стренг, жил, групп, пучков), образующих повив Источник: ГОСТ 15845 80: Изделия кабельные. Термины и определения … Словарь-справочник терминов нормативно-технической документации
Делительная окружность плоского колеса — 78. Делительная окружность плоского колеса Окружность пересечения делительной плоскости плоского колеса дополнительным цилиндром. Примечания: 1. Различают внешнюю, среднюю, внутреннюю и др. делительные окружности плоского колеса, соответствующие… … Словарь-справочник терминов нормативно-технической документации
Делительная окружность кабельного изделия — 1. Окружность, проходящая через центры элементов скрутки (проволок, стренг, жил, групп, пучков), образующих повив Употребляется в документе: ГОСТ 15845 80 Изделия кабельные. Термины и определения … Телекоммуникационный словарь
Окружность, делительная — Делительная окружность Окружность, проходящая через центры элементов скрутки (проволок, стренг, жил, групп, пучков), образующих повив Смотреть все термины ГОСТ 15845 80. ИЗДЕЛИЯ КАБЕЛЬНЫЕ. ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ Источник: ГОСТ 15845 80. ИЗДЕЛИЯ… … Словарь ГОСТированной лексики
Окружность кабельного изделия, делительная — Делительная окружность кабельного изделия … Словарь ГОСТированной лексики
концентрическая окружность конического зубчатого колеса — концентрическая окружность Одна из окружностей пересечения однотипных соосных конусов делительным* (начальным) дополнительным конусом. Примечания 1. Различают концентрические окружности: внешнюю, среднюю, внутреннюю и др. делительные; внешнюю,… … Справочник технического переводчика
2.3. ЭВОЛЬВЕНТНЫЕ ЗУБЧАТЫЕ КОЛЕСА И ИХ ПАРАМЕТРЫ
К основным геометрическим параметрам эвольвентного зубчатого колеса относятся: модуль m, шаг p, угол профиля α, число зубьев z и коэффициент относительного смещения x.
Виды модулей: делительный, основной, начальный.
Для косозубых колес дополнительно различают: нормальный, торцевой и осевой.
Для ограничения числа модулей ГОСТом установлен стандартный ряд его значений, которые определяются по делительной окружности.
Модуль − это число миллиметров диаметра делительной окружности зубчатого колеса, приходящееся на один зуб.
Делительная окружность − это теоретическая окружность зубчатого колеса, на которой модуль и шаг принимают стандартные значения
Делительная окружность делит зуб на головку и ножку.
Начальная окружность – это теоретическая окружность зубчатого колеса, принадлежащая его начальной поверхности.
Головка зуба – это часть зуба, расположенная между делительной ок-ружностью зубчатого колеса и его окружностью вершин.
Ножка зуба – это часть зуба, расположенная между делительной окружностью зубчатого колеса и его окружностью впадин.
Сумма высот головки ha и ножки hf соответствует высоте зубьев h:
Окружность вершин – это теоретическая окружность зубчатого колеса, соединяющая вершины его зубьев.
Окружность впадин – это теоретическая окружность зубчатого колеса, соединяющая все его впадины.
Согласно ГОСТ 13755-81 α = 20°, С* = 0,25.
Коэффициент уравнительного смещения Δу:
Окружной шаг, или шаг p − это расстояние по дуге делительной окружности между одноименными точками профилей соседних зубьев.
Угловой шаг − это центральный угол, охватывающий дугу делительной окружности, соответствующий окружному шагу
Шаг по основной окружности − это расстояние по дуге основной ок-ружности между одноименными точками профилей соседних зубьев
Толщина зуба s по делительной окружности − это расстояние по дуге делительной окружности между разноименными точками профилей одного зуба
S = 0,5 · ρ + 2 · х · m · tg α
Ширина впадины e по делительной окружности − это расстояние по дуге делительной окружности между разноименными точками профилей со-седних зубьев
Толщина зуба Sb по основной окружности − это расстояние по дуге основной окружности между разноименными точками профилей одного зуба.
Толщина зуба Sa по окружности вершин − это расстояние по дуге ок-ружности вершин между разноименными точками профилей одного зуба.
Угол профиля α − это острый угол между касательной t – t к профилю зуба в точке, лежащей на делительной окружности зубчатого колеса и радиус-вектором, проведенным в данную точку из его геометрического центра
Основные параметры, характеризующие зубчатые колеса
Понятия и термины, относящиеся к геометрии и кинематике зубчатых передач, стандартизованы. Стандарты устанавливают термины, определения и обозначения, а также методы расчета геометрических параметров.
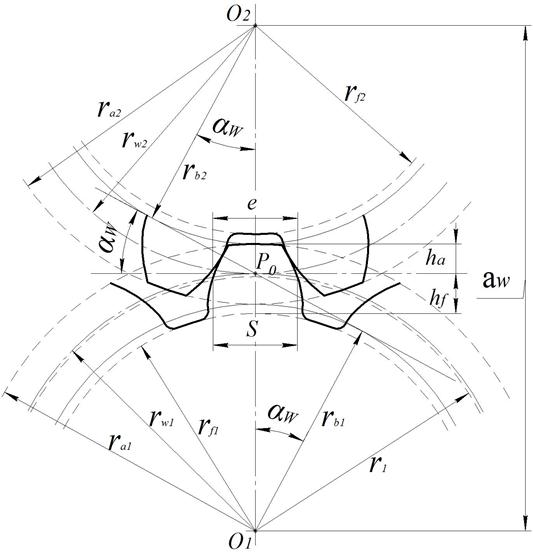
Меньшее из пары зубчатых колес называют шестерней,а большееколесом.Параметрам шестерни приписывают индекс 1, а параметрам колеса – 2. (РИС 5.8).
В зубчатых колесах различают следующие поверхности или окружности: начальная, основная, вершин зубьев, впадин зубьев, делительная.
Начальными ( и ) называются такие окружности (поверхности), которые катятся друг по другу без скольжения, то есть являются центроидами в относительном движении колес. Параметры, относящиеся к начальным окружностям, обозначаются индексом w.
Делительная окружность (поверхность) – это окружность, для которой модуль является стандартным. В некоррегированных, нарезанных несмещенной зубчатой рейкой зубчатых колесах начальная и делительная окружности совпадают. Параметрам, относящимся к делительной окружности или поверхности, дополнительного индекса не приписывают.
Кроме того, различают индексы, относящиеся:
b- к основной поверхности или окружности;
а – к поверхности или окружности вершин (головок) зубьев;
f – к поверхности или окружности впадин (ножек) зубьев.
Зацепление зубчатых колес характеризуется:
и — числами зубьев шестерни и колеса;
— межосевым расстоянием (расстоянием между центрами начальных окружностей);
р – шагом зубьев по делительной окружности (часть делительной окружности, заключенной между одноименными точками двух соседних зубьев);
s– толщина зуба по делительной окружности (дуга делительной окружности вмещающая один зуб);
е – ширина впадины (дуга делительной окружности между двумя соседними зубьями);
— высота ножки зуба (часть профиля зуба внутри делительной окружности);
— высота головки зуба (часть профиля зуба, выступающая за делительную окружность);
— угол зацепления или профильный угол рейки;
Как видно из Рис 5.8, шаг зацепления равен
При передаче непрерывного движения сопряженными колесами шаг зацепления должен быть одинаков для обоих колес. Тогда соотношение между числами зубьев и диаметрами делительных окружностей колес будет:
При определении шага в формулу (5.8) входит трансцендентное число . Это затрудняет подбор размеров зубчатых колес при проектировании. Поэтому для определения размеров колес в качестве основного параметра, определяющего эти размеры, принят модуль зацепления, определяемый как отношение шага зацепления по делительной окружности к числу и округленный до стандартного значения.
Тогда диаметры делительных окружностей, выраженные через модуль, определяться как:
Высота головки зуба
и, как видно из (5.12), будет больше высоты головки на величину осевого смещения, которое для стандартных колес определяется как