Жесткость пружины — формула и примеры расчетов
При внешнем воздействии тело ускоряется либо деформируется. Последнее явление проявляется изменением форм или размеров. Если объект восстанавливается в покое на 100%, деформация называется упругой (резинка), а в остальных случаях — пластической (лепка изделий из глины). Для вычисления первого показателя используется формула жесткости пружины (F = k · x).
Трактовка понятий
В физике упругая деформация возникает из-за силы, равной по модулю оказываемому воздействию. Сила упругости для пружины (F) пропорциональна её удлинению. Для определения жесткости пружины зависимость записывается математически с помощью следующей формулы: F = k·x; где х — длина предмета после его растяжения, а k — коэффициент жесткости.
Формула считается частным случаем закона Гука, который используется для растяжимого тонкого стержня. Чрезмерное воздействие приводит к появлению разных дефектов. Для процесса характерны некоторые особенности, от чего зависит жесткость пружины:
- геометрические параметры детали;
- срок эксплуатации;
- значение коэффициента k, который при определённых условиях способствует снижению сжатия и сохранению силы на одинаковом уровне;
- тип используемого материала (сталь, сплав) в процессе изготовления пружины.
На практических занятиях по физике в 7 классе применяются изделия разных типов. В автомобилестроении используется цветовое обозначение. Для расчета коэффициента жесткости пружины специалисты ориентируются на формулу k=Gd 4 /8D 3 n, где:
- G — определяет модуль сдвига (свойство зависит, к примеру, от используемого сырья);
- d — диаметр куска проволоки (величина определяется в период производства путём проката, а результат записывается в технической документации);
- D — диаметр витков, которые получаются в результате намотки на проволоку (расчет осуществляется с учетом поставленных задач и зависит от нагрузки, оказываемой для сжатия объекта);
- n — количество витков в системе (показатель варьируется в значительном диапазоне, от чего зависят эксплуатационные характеристики предмета).
С помощью формулы может измеряться жёсткость цилиндрической пружины, используемой в разных механизмах. Показатель измеряется в Ньютонах и обозначается Н.
Практические занятия
Механики и физики обозначают с помощью k, c и D коэффициент упругости, пропорциональности, жесткости. Смысл математической записи одинаковый. Численно показатель равняется силе, которая создаёт колебания на одну единицу длины. На практических работах по физике используется в качестве последней величины 1 метр.
Чем выше k, тем больше сопротивление предмета относительно деформации. Дополнительно коэффициент показывает степень устойчивости тела к колебаниям со стороны внешней нагрузки. Параметр зависит от длины и диаметра винтового изделия, количества витков, сырья. Единица измерения жесткости пружины — Н/м.
На практике перед школьниками и механиками может стоять более сложная задача, к примеру, найти общую жёсткость. В таком случае пружины соединены последовательным либо параллельным способом. В первом случае уменьшается суммарная жесткость. Если пружины расположены последовательно, используется следующая формула: 1/k = 1/k1 + 1/k2 + … + 1/ki, где:
- k — суммарная жёсткость соединений;
- k1 …ki — жёсткость каждого элемента системы;
- i — число пружин в цепи.
Если невесомые (расположены горизонтально) предметы соединены параллельно, значение общего k будет увеличиваться. Величина вычисляется по следующей формуле: k = k1 + k2 + … + ki.
Основная методика для вычислений
На практике коэффициент Гука определяется самостоятельно. Для эксперимента потребуется пружина, линейка, груз с определённой массой. Необходимо соблюдать следующую последовательность действий:
Если вышеописанные вычисления произведены, необходимо найти значение коэффициента жёсткости. Используется закон Гука, из которого следует, что k=F/x.
Решение задач
Для нахождения жёсткости в случае использования разных предметов, включая пружинные маятники с разной частотой колебаний, применяется формула Гука либо следствие, вытекающее из неё.
Задача № 1. Пружина имеет длину 10 см. На неё оказывается сила в 100 Н. Изделие растянулось на 14 см. Нужно найти k.
Решение: предварительно вычисляется абсолютное удлинение: 14−10=4 см. Результат переводится в метры: 0,04 м. Используя основную формулу, находится k. Его значение равняется 2500 Н/м.
Задача № 2. На пружину подвешивается груз массой 10 кг. Изделие растягивается на 4 см. Нужно найти длину, на которую растянется пружина, если использовать груз массой в 25 кг.
Решение: Определяется сила тяжести путем умножения 10 кг на 9.8. Результат записывается в Ньютонах. Определяется k=98/0.04=2450 Н/м. Рассчитывается, с какой силой воздействует второй груз: F=mg=245 Н. Для нахождения абсолютного удлинения используется формула x=F/k. Во втором случае х равняется 0,1 м.
Применение цилиндрических пружин
На производстве наиболее востребованы цилиндрические пружины, так как они обладают уникальными особенностями. При создании системы отмечается центральная ось, вдоль которой действуют разные силы. В процессе изготовления подобных изделий используется проволока соответствующего диаметра.
Для её изготовления понадобится специальный сплав либо обычные металлы. Сам материал должен обладать высокой упругостью. Проволока может иметь витки одного диаметра либо разных радиусов. Большим спросом пользуются цилиндрическая пружина, которая в сжатом состоянии обладает незначительной толщиной.
Главными параметрами изделия считаются:
- малый, средний и большой диаметр витков и самой проволоки;
- шаг размещения отдельный колец.
В задачах по физике вычисляется k для двух состояний: растяжение и сжатие. В любом случае используется одна формула для определения величины. Разница понятий:
Отдельно рассматриваются варианты на изгиб и кручение. Такие детали рассчитываются по специальным формулам. Для разных соединений характерны определённые особенности. Чтобы провести определения растяжения, учитывается момент теста.
Показатель зависит от характеристик проволоки, оказываемой силы либо массы тела. Для всех систем используются разные формулы, но полученные результаты не имеют погрешностей. Чтобы провести тесты для вычисления основных параметров, используется специальное оборудование. Простые задачи с деформацией пружин решают ученики на уроках физике в 7−8 классе. О параллельном и последовательном соединении элементов системы узнают учащиеся старших классов.
Сила упругости. Закон Гука
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Сила упругости. Закон Гука»
В данной теме речь пойдёт о силах упругости, а также о законе Гука.
Ранее говорилось, что основными силами в механике являются гравитационные силы, силы упругости и силы трения.
Известно, что одно из проявлений взаимодействия тел — это их деформация. Деформацией называют изменение формы и размеров тела, происходящее из-за неодинакового смещения различных частей одного тела в результате воздействия другого тела.
Рассмотрим, почему деформации неодинаковы у различных тел?
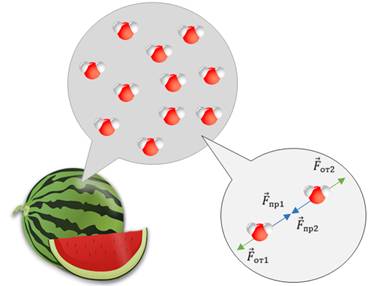
Чтобы ответить на этот вопрос, вспомним о строении вещества. Все вещества состоят из частиц (молекул, атомов, ионов), между которыми существуют силы взаимодействия. Это силы электромагнитной природы, которые в зависимости от расстояния между частицами проявляются то как силы притяжения, то как силы отталкивания. Если воздействие на тело вызывает увеличение расстояния между молекулами, то силы межмолекулярного притяжения препятствуют этому. Уменьшению расстояния между молекулами противодействуют силы отталкивания. Так вот, чтобы не рассматривать сложные электромагнитные взаимодействия, в механике для характеристики этих явлений и вводят силу упругости.
Силой упругости называется сила, возникающая при деформации любых твердых тел, а также при сжатии жидкостей и газов. Сила упругости препятствует изменению размеров и формы тела.
Также следует помнить, что силы упругости всегда перпендикулярны поверхности соприкосновения взаимодействующих тел, а если во взаимодействии участвуют такие тела, как пружины или нити, то силы упругости направлены вдоль их оси.
Рассмотрим, какую роль играет эта сила при взаимодействии тел. Проведём следующий опыт. Прикрепим к бруску, лежащему на столе, резиновый шнур (с метками на одинаковом расстоянии друг от друга) и медленно начнем тянуть его в горизонтальном направлении. Под действием силы шнур растягивается, и только когда весь шнур растянется на некоторую величину, брусок придет в движение. Как это объяснить?
При растяжении шнура происходит смещение одних его частей относительно других, в результате чего в шнуре возникает сила упругости, равная по величине деформирующей силе. С этого момента шнур играет роль «передающего звена». Такие же явления всегда происходят, когда движение от одного тела к другому передается при помощи «связей», то есть нитей, шнуров, пружин, тросов, различных сцепок и так далее.
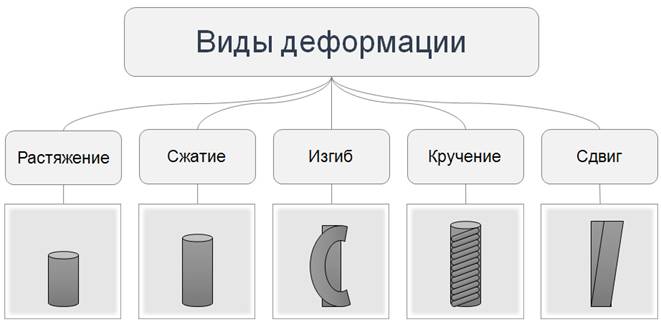
По характеру смещения частей тела (а вернее, молекулярных слоев внутри него) друг относительно друга различают несколько видов деформации: растяжение, сжатие, изгиб, кручение, сдвиг.
При деформации растяжения расстояние между молекулярными слоями увеличивается. Такую деформацию испытывают, например, тросы подъемных кранов, канатных дорог, буксирные тросы, струны музыкальных инструментов.
А при деформации сжатия расстояние между молекулярными слоями уменьшается. Сжатию, например, подвергаются стены и фундаменты зданий.
Если в результате воздействия одни молекулярные слои растягиваются, а другие сжимаются, то наблюдается деформация изгиба. Деформацию изгиба испытывают на себе балки перекрытий в зданиях и мостах.
При деформации кручения происходит поворот одних молекулярных слоев относительно других. А если одни слои молекул смещаются относительно других, то происходит деформация сдвига.
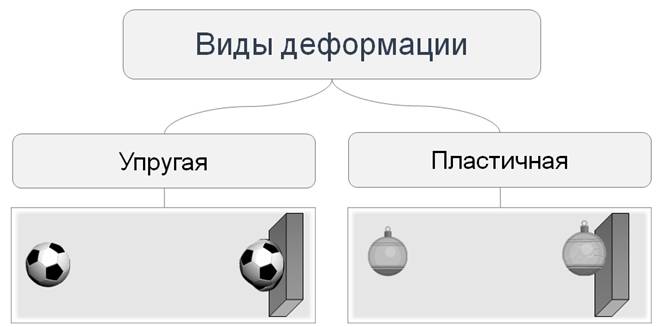
По мимо этого, деформации также разделяют на упругие и неупругие, или пластичные.
Деформация называется упругой, если после прекращения воздействия тело полностью восстанавливает первоначальные форму и размеры.
А если этого не происходит, то деформация называется неупругой или пластичной.
Конечно же, деформация конкретного тела может быть, как упругой, так и неупругой, так как ее характер зависит не только от свойств тела, но и от величины воздействия на него.
Различные виды деформаций возникают в любых сооружениях и механизмах, и необходимо установить законы, которые позволят рассчитать величину этих деформаций.
Наиболее часто встречаются и достаточно просто математически описываются упругие деформации растяжения или сжатия.
Если взаимодействие этих тел друг с другом ничем не отличается, то каково ускорение третьего тела при его взаимодействии с одним из первых двух?
Проведем опыт. Прикрепим один конец резинового шнура с метками к вертикальной стенке, а другой — к динамометру, на который будем действовать силой. Расположим под шнуром линейку. Определяя силу, действующую на конец шнура, по динамометру, будем фиксировать смещение конца шнура вдоль линейки и изменение расстояний между метками.
Общее удлинение шнура, определяемое по смещению его конца, является суммой удлинений всех его частей. Аналогично общее укорочение, например, при сжатии пружины, является суммой уменьшений расстояний между всеми ее витками.
Если обозначить начальную длину шнура через l, а конечную длину — через l, то для характеристики деформаций растяжения или сжатия можно ввести абсолютное удлинение ∆l, равное модулю разности между конечной и начальной длиной тела.
Если шнур под действием деформирующей силы больше не удлиняется, то ее действие уравновешивает упругая сила.
Первое по-настоящему научное исследование процесса упругого растяжения и сжатия вещества предпринял Роберт Гук. Он установил экспериментально, что при малых деформациях растяжения или сжатия абсолютное удлинение тела прямо пропорционально деформирующей силе.
На практике часто необходимо определить силу упругости, возникающую в теле при его деформации, и закон Гука формулируют следующим образом: модуль силы упругости, возникающей при малых деформациях сжатия или растяжения тела, прямо пропорционален величине абсолютного удлинения.
где k — это коэффициент пропорциональности, называемый жесткостью тела.
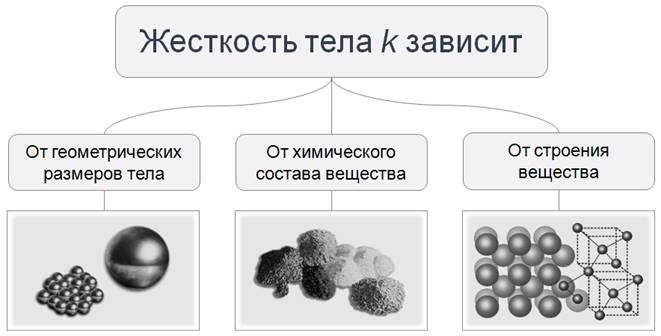
Жесткость является характеристикой данного тела (пружины, шнура, стержня) и зависит от его поперечных и продольных размеров, химического состава, и строения вещества, из которого тело изготовлено.
Единицей измерения жесткости в системе СИ, является Н/м (ньютон на метр).
При расчетах движения тел под действием силы упругости необходимо учитывать ее направление. Если выбрать начало отсчета под крайней точкой недеформированного тела, то абсолютное удлинение можно характеризовать координатой конца деформированного тела.
При растяжении и при сжатии образца сила упругости направлена противоположно смещению его конца. Тогда можно записать закон Гука для проекции силы упругости на выбранную координатную ось в виде:
Ту или иную форму записи закона Гука используют в зависимости от условия задачи и величины, которую нужно определить.
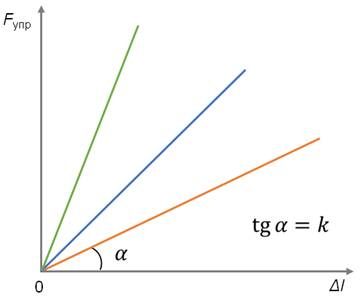
Графиком зависимости силы упругости от абсолютного удлинения тела является прямая линия, угол наклона которой к оси абсцисс зависит от коэффициента жесткости k.
Сила упругости, как и любая из сил, рассматриваемых в механике, подчиняется законам Ньютона, а по закону Гука можно рассчитать деформации, возникающие при взаимодействиях тел. Однако необходимо отметить, что закон Гука хорошо выполняется только при малых деформациях.
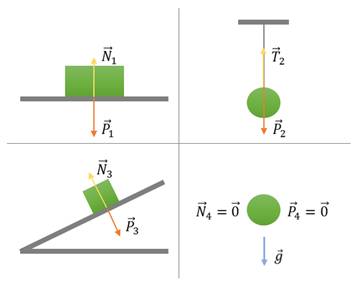
Частным случаем проявления силы упругости является вес тела. Вес тела — это сила, с которой тело, вследствие своего притяжения к Земле, действует на неподвижную относительно него опору или подвес.
Вес тела возникает вследствие его деформации, вызванной действием силы со стороны опоры (силы нормальной реакции опоры) или подвеса (силы натяжения).
Следует помнить, что сила веса существенно отличается от силы тяжести. Во-первых, вес тела обусловлен силой тяготения и межмолекулярными силами в веществе, то есть это сила электромагнитной природы. А сила тяжести — это гравитационная сила.
Во-вторых, они приложены к разным телам: сила тяжести приложена к телу, а вес — к опоре или подвесу.
В-третьих, направление силы веса тела не обязательно совпадает с отвесным направлением.
Сила тяжести, действующая на тело в данном месте Земли постоянна, и не зависит от характера движения тела. Вес зависит от ускорения, с которым движется тело.
Сила упругости
Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Силы, возникающие при пластических деформациях, не относятся к силам упругости.
Понятие о деформациях
Деформация — это изменение формы и размеров тела.
К деформациям относятся: растяжение, сжатие, кручение, сдвиг, изгиб.
Деформации бывают упругими и пластическими.
Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину (displaystyle x) (разница между крайними положениями), сила упругости задается формулой [F=kx] где (displaystyle k) — коэффициент жесткости пружины.
Единицы измерения коэффициента жесткости: (k=) [Н/м].
Закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела.
Кубик массой (M = 2) кг, сжатый с боков пружинами, покоится на гладком горизонтальном столе. Первая пружина сжата на 2 см, а вторая сжата на 6 см. Жёсткость первой пружины (k_1 = 1200) Н/м. Чему равна жёсткость второй пружины (k_2) ? Ответ выразите в Н/м.
По второму закону Ньютона силы упругости пружин будут уравновешивать друг друга, следовательно: [k_1Delta x_1=k_2Delta x_2] где (Delta x_1) и (Delta x_2) – сжатие первой и второй пружины соответственно.
Откуда жесткость второй пружины [k_2=dfrac
На штативе закреплён школьный динамометр. К нему подвесили груз массой 0,1 кг. Пружина динамометра при этом удлинилась на 2,5 см. Чему будет равно удлинение пружины, если масса груза увеличится втрое? (Ответ дайте в сантиметрах)
Согласно закону Гука [F=kDelta x] где k – жесткость пружины, ( Delta x) – удлинение пружины.
Найдем жесткость пружины, зная, что ( Delta x) = 2,5 см = 0,025 м при приложении силы, равно ( F=m_1g=0,1cdot 10=1text < H>) : [k=dfrac
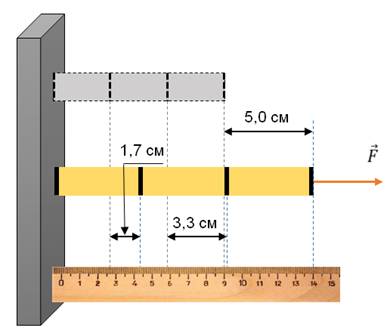
К системе из кубика массой M = 3 кг и двух пружин приложена постоянная горизонтальная сила F величиной 20 Н (см. рисунок). Между кубиком и опорой трения нет. Система покоится. Жёсткость первой пружины (k_1 = 400 text< Н/м>) . Жёсткость второй пружины (k_2 = 800 text< Н/м>) . Каково удлинение первой пружины? (Ответ дайте в сантиметрах)
Согласно закону Гука удлинение (Delta x) пружины связано с ее жесткостью k и приложенной к ней силе F выражением (F=kDelta x) . На первую пружину действует такая же сила F, что и на вторую, так как трения между кубиком и опорой нет. То, что первая пружина соединена со второй через кубик, здесь не имеет никакого значения, соответственно удлинение первой пружины – это величина, равная: [Delta x=dfrac