Виды и методы силового расчета рычажных механизмов
Постановка задачи силового расчета: для исследуемого механизма при известных геометрических, кинематических и инерционных характеристиках и внешних силах: определить уравновешивающую силу или момент (управляющее силовое воздействие) и реакции в кинематических парах механизма.
Виды силового расчета:
- статический — для механизмов находящихся в покое или движущихся с малыми скоростями, когда инерционные силы пренебрежимо малы, или в случаях, когда неизвестны массы и моменты инерции звеньев механизма (на этапах, предшествующих эскизному проектированию); Уравнения статического равновесия:
где Fi — внешние силы, приложенные к механизму или его звеньям,
Mi— внешние моменты сил, приложенные к механизму или его звеньям.
- кинетостатический — для движущихся механизмов при известных массах и моментах инерции звеньев, когда пренебрежение инерционными силами приводит к существенным погрешностям; Уравнения кинетостатического равновесия:
где Fиi-инерционные силы, приложенные к звеньям,
Mиi-моменты сил инерции, приложенные к звеньям.
- кинетостатический с учетом трения — может быть проведен, когда определены характеристики трения в КП и размеры элементов пар.
Методы силового расчета:
- метод проекций (аналитический)
- метод планов сил (графо-аналитический)
6. Кинетостатический силовой расчет рычажных механизмов методом планов сил.
Порядок (последовательность) силового анализа рычажного механизма:
· Выделяем из механизма последнюю (крайнюю, наиболее удаленную от ведущего звена) структурную группу и проводим её силовой расчёт. Для этого:
· прикладываем все внешние силы, действующие на звенья группы;
· действие отсоединенных звеньев заменяем их реакциями;
· прикладываем силы и моменты инерции;
· определяем реакции, используя уравнения статики
· Выделяем из механизма следующую структурную группу и проводим её силовой расчёт в таком же порядке.
· Силовой расчёт заканчиваем силовым расчётом ведущего звена.
Для механизмов 2-го класса для каждого вида разработан свой алгоритм определения реакций в кинематических парах. Рассмотрим примеры.
Пример 1.
Структурная группа 2-го класса, 1-го вида (рис. 7.5, а,б)
Fi,1 t определяется из уравнения моментов для звена 1 — ∑МB=0 относительно т. В. (рис.7.5, а);
Fj,2 t определяется из уравнения моментов для звена 2 — ∑МВ=0 относительно т. В (рис.7.5,а).
Fi,1 n и Fj,2 n определяются из плана сил (рис.7.5,б), полученного на основе векторного уравнения;
∑Fk=0, где Fk – силы, действующие на структурную группу.
Структурная группа 2-го класса, 2-го вида (рис.7.6, а, б)
Fj,2 определяется из уравнения моментов — ∑МА=0 относительно т. А. Fi,1=Fi,1 n +Fi,1 t определяется из плана сил (рис.7.6,б) на основе векторного уравнения ∑Fk=0.
Структурная группа 2-го класса, 3-го вида (рис.7.7, а)
Входное (начальное) звено (рис.7.8, а).
Мур определяется из уравнения моментов — ∑Мо=0.
Теорема о «жестком рычаге» Жуковского используется для определения уравновешивающей силы или уравновешивающего момента без предварительного определения реакций в кинематических парах механизма и является графической интерпретацией принципа возможных перемещений точек приложения сил. Для реального механизма эти возможные перемещения являются реальными.
Исходя из принципа сохранения энергии сумма работ всех внешних сил, приложенных к звеньям механизма, равна нулю. Это условие можно записать в виде
где Pi – все внешние силы, в том числе силы полезного и вредного сопротивления, силы инерции и веса, действующие на звенья механизма (силы реакции здесь не учитываются);
dSi – элементарные перемещения точек приложения этих сил;
ai – угол приложения внешних сил, или угол давления (угол между вектором силы и вектором скорости).
Разделим уравнение (3.7) на бесконечно малый интервал времени dt и получим (при условии, что dS/dt = )
то есть сумму мгновенных мощностей, равную нулю.
Для определения величины мгновенных мощностей можно выполнить решение в следующей графической интерпретации.
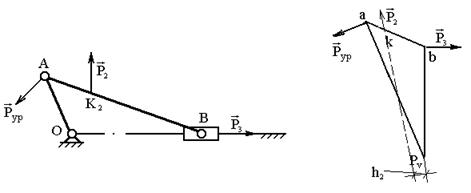
Дано звено с известной скоростью точки В и приложенной к этой точке силой (рис. 3.13). Построим план скоростей, повёрнутый на 90 0 , где , . Вычислим момент силы относительно полюса Рv плана скоростей:
С учётом этого уравнение (3.8) можно записать как .
Так как масштаб , то можно сформулировать теорему Жуковского:
или алгебраическая сумма моментов всех внешних сил (включая силы инерции), перенесенных с механизма в соответствующие точки повёрнутого на 90 0 плана скоростей, относительно полюса равна нулю.
Последовательность определения Pур в механизме по теореме Жуковского:
1. Построить повёрнутый на 90 0 (в любую сторону) план скоростей механизма.
2. В соответствующие точки плана скоростей нанести все ранее определённые внешние силы (включая силы инерции и силы веса), действующие на механизм, в том числе и уравновешивающую силу Pур.
3. Составить уравнение вида (3.9). Плечи моментов сил брать из повёрнутого плана скоростей.
4. Из составленного уравнения определить Pур.
Пример 2.Заданы внешние силы, действующие на звенья механизма Р2 и Р3. Найдём уравновешивающую силу Рур, для чего построим план механизма в масштабе длин (рис. 3.14) и повёрнутый на 90 0 план скоростей (рис. 3.15).
Приложим силы в соответствующие точки k и b3 повёрнутого плана скоростей, обозначаем плечи сил. Составляем уравнение моментов сил относительно полюса плана скоростей:
Рис. 3.14. План механизма Рис. 3.15. Повёрнутый на 90 0
Если сила Pур получается с отрицательным знаком, то её предварительно выбранное направление следует поменять на противоположное.
8. Силовой анализ рычажных механизмов с учетом сил трения
Трение в поступательной кинематической паре
При перемещении одного тела (звена механизма) относительно находящегося с ним в контакте другого тела (звена) в месте их контакта возникает сила, сопротивляющаяся перемещению, – сила трения F (рис. 3.16).
Величину коэффициента трения в поступательной кинематической паре можно определить с помощью так называемого закона Кулона, в соответствии с которым величина силы трения F прямо пропорциональна нормальной силе N между соприкасающимися звеньями. Векторная сумма сил и равна полной силе реакций в кинематической паре: (рис. 3.16).
Отношение называют коэффициентом трения скольжения в поступательной кинематической паре, а угол – углом трения скольжения.
Полная реакция отклоняется на угол трения в сторону, противоположную скорости (см. рис. 3.16).
Величину коэффициента трения скольжения f можно определить экспериментально или по справочникам (величина f зависит от шероховатости, материалов, трущихся поверхностей, наличия смазки, ее качества, температуры и т.д.).
 | |
| Рис. 3.16. Схема сил в поступательной кинематической паре | Рис. 3.17. Схема сил во вращательной кинематической паре |
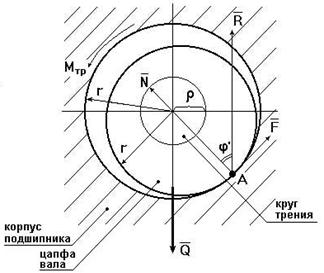
Трение во вращательной кинематической паре
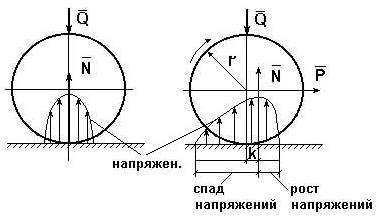
Внешние нагрузки, действующие на вал при его вращении, показаны на схеме рис. 3.17. Здесь А – точка приложения нормальной реакции , причем – равно-действующая всех нор-мальных сил (эпюра этих сил может иметь различный вид), (рис. 3.18); – сила трения (равно-действующая всех сил трения, распределенных по поверхности контакта); – сила давления цапфы вала на опору (корпус подшипника); – сила реакции во вращательной кинематической паре, ; ; – угол трения; r – радиус цапфы (опорной части) вала; – радиус круга трения; – приведенный коэффициент трения.
Во вращательной кинематической паре (см. рис. 3.15) реакция отстоит от оси вращения на величину радиуса круга трения , причем всегда касательна к кругу трения.
Величину можно определить экспериментально или по эмпирическим формулам с учетом износа подшипника и соответствующего изменения эпюр давления (рис. 3.18): для нового подшипника , для изношенного – , где f – коэффициент трения скольжения в поступательной кинематической паре (берется из справочников).
Рис. 3.18. Примерные схемы эпюр давления в новом и изношенном подшипниках скольжения
Трение качения в высшей кинематической паре
Картину внешних сил и эпюр распределения давлений в месте контакта тел качения можно условно отобразить на нижеприведенных схемах (рис. 3.19). В состоянии покоя эпюра напряжений в зоне контакта симметрична относительно общей нормали, проведенной через условную точку касания, а равнодействующая сила N совпадает с нормалью. При качении симметрия эпюры нарушается, а сила N смещается в направлении качения на расстояние k.
Рис. 3.19. Примерные схемы сил и эпюр давления
в зоне контакта цилиндра с плоскостью: а – состояние покоя;
б – состояние перекатывания
Здесь – равнодействующая сила давлений в месте смятия соприкасающихся звеньев (тел качения); – нагружающая сила, ; – момент трения качения; – плечо силы трения качения или коэффициент трения качения (имеет размерность длины); – сила перекатывания.
Условие равновесия перекатывающегося тела в форме моментов можно записать как , откуда .
Силовой расчёт рычажного механизма
Пояснительная записка сдаётся по разделам вместе с соответствующими листами.
Защита курсовой работы – на 17 неделе учебного семестра.
2. содержание листа 1
2.1. исходные данные:
– структурная схема рычажного механизма;
– координаты элементов стойки;
– некоторые размеры звеньев;
– угловая скорость кривошипа ω к;
– величина, направление и точка приложения силы полезного сопротивления Fпс;
– угол jп поворота кривошипа на рабочем ходу от положения, соответствующего началу рабочего хода до расчётного (задаётся преподавателем);
– удельная масса звеньев q = 30 кг/м.
ПОРЯДОК ВЫПОЛНЕНИЯ
2.2.1. Структурный анализ и геометрический синтез
рычажного механизма:
– вычертить структурную схему, указав номера и названия звеньев;
– описать принцип работы всей технологической машины и, в частности, рычажного механизма;
– составить таблицу кинематических пар;
– вычислить подвижность механизма;
– расчленить механизм на простейшие структурные составляющие и вычертить их, указав наименования;
– написать формулу строения механизма и определить его класс;
– если не известны какие-либо размеры звеньев, определить их.
Кинематический анализ рычажного механизма
2.2.2.1. Определение положений звеньев и заданных точек:
– вычертить планы механизма в крайних положениях;
– определить величину хода или размаха выходного звена, а также углы поворота кривошипа, соответствующие рабочему (αр) и холостому (αх) ходам. Проставить соответствующие размеры на чертеже;
– задать направление вращения кривошипа, исходя из минимизации мощности, потребляемой механизмом;
– вычислить коэффициент изменения средней скорости выходного звена;
– построить план механизма в расчётном положении;
– взяв за начало отсчёта положение выходного звена в момент начала рабочего хода, измерить его перемещение или угол поворота в расчётном положении,.
2.2.2.2. Определение скоростей:
– для режима установившегося движения (при постоянной заданной угловой скорости вращения кривошипа) построить план скоростей механизма в расчётном положении;
– определить величины линейных скоростей подвижных центров шарниров, а также точки приложения силы полезного сопротивления Fпс;
– вычислить значения угловых скоростей всех звеньев, совершающих вращательное или плоское движение, определить их направления и обозначить на плане механизма.
2.2.2.3. Определение ускорений:
– построить план ускорений для расчётного положения;
– определить величины тангенциальных составляющих ускорений центров подвижных шарниров, а также ускорение точки приложения силы Fпс;
– вычислить значения угловых ускорений всех звеньев, совершающих вращательное или плоское движение, определить их направления и обозначить на плане механизма;
– уточнив при необходимости размеры звеньев, определить ускорения их центров масс, кроме кривошипа, считая, что они расположены посередине каждого звена. Если звено состоит из двух стержней сопоставимой длины, не расположенных на одной прямой, ускорения определяют по отдельности для каждого стержня.
Силовой расчёт рычажного механизма
2.2.3.1. Определить массы и силы веса всех подвижных звеньев, кроме кривошипа, а также действующие на них силы и моменты пар сил инерции в расчётном положении. Массы ползунов, не представляющих собой стержни, принять равными массам соединённых с ними шатунов. Массами камней и роликов пренебречь.
2.2.3.2. Нанести все активные силы и инерционную нагрузку на план механизма. Уравновешивающую силу считать приложенной в конце кривошипа и направленной перпендикулярно ему.
2.2.3.3. Вычертить планы структурной группы, входного звена, а также одного из звеньев, входящих в структурную группу;
2.2.3.4. Нанести на эти планы все активные силы, инерционную нагрузку и реакции связей от соседних звеньев;
2.2.3.4. Построив необходимое количество планов сил, определить по ним величины и направления всех реакций связей, а также величину уравновешивающей силы.
2.2.3.5. Построить рычаг Жуковского и также определить величину уравновешивающей силы.
2.2.3.6. Вычислить относительную погрешность определения уравновешивающей силы двумя способами. Если расхождение превышает 5%, найти и устранить ошибку.
ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ
2.3.1. Пункт 2.2.1 выполняется в пояснительной записке, графическая часть остальных – на листе формата А1. Графические построения могут выполняться как вручную (карандашом), так и на компьютере с использованием одного из графических редакторов.
2.3.2. Примерная толщина линий: 0,8 мм – для осей координат и кривых на графиках; 0,4 мм – для планов механизма, скоростей, ускорений, сил, а также рычага Жуковского; 0,2 мм – все прочие линии.
2.3.3. Яркость линий разной толщины должна быть одинаковой.
2.3.4. Над каждым рисунком должна быть надпись шрифтом № 7 с указанием под ней масштабного коэффициента построения шрифтом № 5.
2.3.5. Значения масштабных коэффициентов выбираются из ряда, рекомендованного для ТММ: 1; (1,25; 1,5; 1,75); 2; 2,5; 4; 5; (8) с последующим умножением на 10 в любой целой степени. Их величины принимаются таким образом, чтобы обеспечить максимальное заполнение листа.
2.3.6. Пояснительная записка выполняется согласно СТП 1.01 – 2002.
2.3.7. Номера чертежей в основных надписях расшифровываются согласно следующему примеру:
номер ТММ.30.06.01.
ТММ – название дисциплины;
30 – номер схемы рычажного механизма;
06 – номер варианта (строки в задании);
01 – номер листа графической части курсовой работы.
СОДЕРЖАНИЕ ЛИСТА 2
3.1. ИСХОДНЫЕ ДАННЫЕ:
– структурная схема зубчатого механизма;
– известные числа зубьев колёс
– угловая скорость выходного вала, равная ω к;
– направление вращения кривошипа (с листа 1);
– модуль зубьев m;
– исходный контур по ГОСТ 13755–81;
– критерии качества: примерное равенство удельных скольжений и максимально возможный коэффициент перекрытия.
ПОРЯДОК ВЫПОЛНЕНИЯ
3.2.1. Исходя из условия соосности, определить неизвестное число зубьев одного из колёс.
3.2.2. Вычислить передаточное отношение механизма и, учитывая, что он представляет собой редуктор, установить, какой из валов является входным, а какой – выходным.
3.2.3. Определить аналитически угловые скорости всех звеньев механизма.
3.2.4. Проверить правильность кинематического расчёта графическим методом.
3.2.5. Вычислить относительные погрешности между угловыми скоростями, определёнными разными методами. Если для какого-либо звена она превышает 5%, найти и устранить ошибку.
3.2.6. Исходя из заданных критериев качества, определить коэффициенты смещения колёс, составляющих непланетарную ступень механизма, и выполнить её геометрический расчёт.
3.2.7. Вычислить ожидаемые качественные показатели зацепления.
3.2.8. Разместить в пояснительной записке таблицу параметров зацепления.
3.2.9. Выбрав походящий масштаб, вычертить чертёж зацепления с указанием стандартных условных обозначений всех вычисленных размеров.
ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ
3.3.1. Формат листа графической части А 2.
3.3.2. Выполнять п. 2.3, кроме п. 2.3.2.
3.3.3. Примерная толщина линий: 0,8 мм – для плана механизма, для планов линейных скоростей и картины угловых скоростей, для окружностей вершин и впадин; 0,4 мм – для таблиц; 0,2 мм – все прочие линии.
3.3.4. При выполнении п. 3.2.9 использовать один из масштабов ЕСКД или ТММ, подобрав его таким образом, чтобы межцентровое расстояние на чертеже находилось в ориентировочных пределах от 300 до 400 мм.
4. литература, рекомендуемая для ВЫПОЛНЕНИЯ курсовоЙ РАБОТЫ
Основные пособия
4.1.* Солнцев Б.А. Анализ четырёхшарнирных механизмов. – Рыбинск: РГАТУ, 2012. – 80 с. (Лист 1).
4.1.* Солнцев Б.А. Анализ кривошипно-ползунных механизмов. – Рыбинск: РГАТУ, 2013. – 72 с. (Лист 1).
4.1.* Солнцев Б.А. Анализ кривошипно-кулисных механизмов. – Рыбинск: РГАТУ, 2013. – 64 с. (Лист 1).
4.2. Солнцев Б.А. Практикум по кинематическому анализу зубчатых механизмов. – Рыбинск: РГАТА, 2003. – 52 с. (Лист 2).
4.3. Солнцев Б.А. Синтез эвольвентных зубчатых зацеплений. – Рыбинск: РГАТА, 2005. – 52 с. (Лист 2).
4.4. СТП 1.01–2002. Общие требования к оформлению учебных документов. Текстовые документы. – Рыбинск: РГАТА, 2002. – 32 с. (Пояснительная записка).
* Конкретное название определяется видом рычажного механизма в задании на курсовую работу
Дополнительные пособия
4.5. Солнцев Б.А. Кинематика механизмов: Лабораторный практикум по ТММ. – Рыбинск: РГАТА, 2002. – 58 с. (Лист 1).
4.6. Солнцев Б.А. Силовой анализ двухподвижных рычажных механизмов. – Рыбинск: РГАТА, 2001. – 47 с. (Лист 1).
4.7. Солнцев Б.А. Основы кинематического анализа зубчатых механизмов. – Рыбинск: РГАТА,1994. – 52 с. (Лист 2) – вместо 4.2.
ЭТАПЫ РАСЧЕТА РЫЧАЖНОГО МЕХАНИЗМА
В указаниях даны рекомендации по разработке компьютерной программы для расчета рычажного механизма на базе использования аналитических методов расчета. Методика предполагает сочетание самостоятельной разработки студентом отдельных фрагментов программы с использованием стандартных процедур, разработанных на кафедре ОКММ.
Особое внимание уделяется контролю правильности результатов, полученных на всех этапах комплексного расчета.
СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМА
Анализ следует выполнять в такой последовательности:
— изобразить структурную схему механизма;
— присвоить стойке номер , назначить начальное звено и присвоить ему номер 1;
— проанализировать характер движения звеньев и записать их названия;
— дать буквенные обозначения вращательным и поступательным кинематическим парам;
— выделить первую присоединенную двухзвенную структурную группу, последовательно пронумеровать звенья и определить ее вид по классификации Ассура-Артоболевского;
— продолжить выделение следующих структурных групп до исчерпания всех звеньев механизма;
— записать формулу строения механизма;
— составить таблицу кинематических пар, включающую их буквенные обозначения, номера образующих их звеньев и их вид (вращательная или поступательная);
— проконтролировать число степеней свободы механизма с помощью формулы Чебышева.
Более подробно с порядком структурного анализа механизмов можно ознакомиться по методическим указаниям [1].
ТЕХНИЧЕСКОЕ И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
ПРОЕКТИРОВАНИЯ
Для выполнения курсового проекта необходимо иметь:
— систему Turbo Pascal, включающую файлы Turbo.exe, Turbo.tpl, Graph.tpu и EgaVga.bgi, общим объемом около 200 КВ;
— исходную программу Mechan1.pas;
— модули MPF.tpu, Dinamika.tpu и TMM3m.tpu, содержащие стандартные процедуры общим объемом около 160 КВ.
Необходимо знать основы программирования на языке Turbo Pascal, а также основные приемы работы с системой Turbo Pascal [2].
5 СТРУКТУРА ПРОГРАММЫ
Структуру программы рассмотрим на примере исходной программы Mechan1.pas. Ниже приводится сокращенный текст программы, содержащий подробные комментарии, которых нет в исходном файле. Эти комментарии набраны курсивом и заключены в фигурные скобки.
Uses Crt, Graph, MPF, Dinamika, TMM3m;< Перечень модулей >
Var Xo, Yo, LOA, FiOA0g, dFi, m2, Is2 : Real;< Описание переменных>
Xs2, Ys2 – координаты точки S, принадлежащей звену 2;
Xs2_1, Ys2_1 — передаточные функции первого порядка (ПФ1) точки S2;
Xs2_2, Ys2_2 — передаточные функции второго порядка (ПФ2) точки S2;
FiABg, FiABr — угол, образуемый осью звена АВ с положительным направлением оси абсцисс, в градусах и радианах (угловая ПФ0 звена);
FiAB_1, FiAB_2 — угловые ПФ1 и ПФ2 звена АВ >
Var Xa, Ya, Xa_1, Ya_1, Xa_2, Ya_2 : Massiv;< Описание ПФ т. А >
Var FiABg, FiABr, FiAB_1, FiAB_2 : Massiv;< Описание ПФ угла АВ >
Var G2y, G3y, G4y, G5y : Real;< Описание сил тяжести >
Begin
InitGraph (Driver, Mode, ’’);
SetBKcolor(7);
For i:=1 to m+1 Do Begin
Str (i:2, StrVar);
YO:=0;
Str (Fioag[i]:8:4, StrVar);
SetColor (15);
Kriv (Xo, Yo, Loa, Fioag[i], q, jk, Mas,< Входные данные >
lc:=75; Ori:=1;
TestPF (m, Xa, Xa_1, Xa_2, ‘Xa’);
Grafik (m+1, FiOAg, Xa, Xa_1, Xa_2, ’Xa’, ’Xa_1’, ’Xa_2’);
TestPF (m, Ya, Ya_1, Ya_2, ‘Ya’);
Grafik (m+1, FiOAg, Ya, Ya_1, Ya_2, ’Ya’, ’Ya_1’, ’Ya_2’);
m3:=200;
m4:=300;
m5:=1200;
Is3:=0.5;
Is4:=0.9;
G3y:=-m3*g;
G4y:=-m4*g;
G5y:=-m5*g;
For i:=1 to m+1 Do Begin
G3y*Ys3_1[i]+
G4y*Ys4_1[i]+
G5y*Ys5_1[i])/1000;
Ip2[i]:=(m2*(sqr(Xs2_1[i])+sqr(Ys2_1[i]))+
m3*(sqr(Xs3_1[i])+sqr(Ys3_1[i]))+
m4*(sqr(Xs4_1[i])+sqr(Ys4_1[i]))+
m5*(sqr(Xs5_1[i])+sqr(Ys5_1[i]))/1000000+
Is2*sqr(FiAB_1[i]);
Ip2_1[i]:= 2*(m2*(Xs2_1[i]*Xs2_2[i]+Ys2_1[i]*Ys2_2[i])+
m3*(Xs3_1[i]*Xs3_2[i]+Ys3_1[i]*Ys3_2[i])+
m4*(Xs4_1[i]*Xs4_2[i]+Ys4_1[i]*Ys4_2[i])+
m5*(Xs5_1[i]*Xs5_2[i]+Ys5_1[i]*Ys5_2[i]))/1000000+
2*Is2*FiAB_1[i]*FiAB_2[i];
For i:=1 to m+1 Do Begin
as2y:=(Ys2_2[i]*sqr(Om1[i])+Ys2_1[i]*e1[i])/1000;
as3x:=(Xs3_2[i]*sqr(Om1[i])+Xs3_1[i]*e1[i])/1000;
as3y:=(Ys3_2[i]*sqr(Om1[i])+Ys3_1[i]*e1[i])/1000;
as4x:=(Xs4_2[i]*sqr(Om1[i])+Xs4_1[i]*e1[i])/1000;
as4y:=(Ys4_2[i]*sqr(Om1[i])+Ys4_1[i]*e1[i])/1000;
as5x:=(Xs5_2[i]*sqr(Om1[i])+Xs5_1[i]*e1[i])/1000;
as5y:=(Ys5_2[i]*sqr(Om1[i])+Ys5_1[i]*e1[i])/1000;
F2y[i]:=-m2*as2y;
F3x[i]:=-m3*as3x;
F3y[i]:=-m3*as3y;
F4x[i]:=-m4*as4x;
F4y[i]:=-m4*as4y;
F5x[i]:=-m5*as5x;
F5y[i]:=-m5*as5y;
Mf2[i]:=-Is2*e2;
End;
For i:=1 to m+1 Do
Pogr1[i]:=Mpd[i] + Mnc[i] + Mf1[i]+
(F2x[i]*Xs2_1[i] + F2y[i]*Ys2_1[i] +
F3x[i]*Xs3_1[i] + F3y[i]*Ys3_1[i] +
F4x[i]*Xs4_1[i] + F4y[i]*Ys4_1[i] +
F5x[i]*Xs5_1[i] + F5y[i]*Ys5_1[i])/1000 +
Mf2[i]*FiAB_1[i];
Grafik (m+1, Fioag, Pogr1, zz, zz, ’Pogr1’, ’’, ’’);
For i:=1 to n+1 Do
PogrGlob[i]:=Mpd[i]+Mf1[i]+(R12x[i]*(Yo-Ya[i]-R12y[i]*(Xo-Xa[i]))/1000;
Grafik (m+1, FiOAg, PogrGlob, zz, zz, ’PogrGlob’, ’’, ’’);
6 СТАНДАРТНЫЕ ПРОЦЕДУРЫ ДЛЯ РАСЧЕТА
СТРУКТУРНЫХ ЭЛЕМЕНТОВ МЕХАНИЗМА
Стандартные процедуры для расчета передаточных функций структурных элементов рычажных механизмов разработаны на основе аналитических методов. ПФ0 представляют собой зависимости углов звеньев и координат характерных точек от геометрических параметров элементов внешних кинематических пар, полученных на основе простых геометрических соотношений. ПФ1 и ПФ2 получены посредством последовательного дифференцирования этих выражений по обобщенной координате. Так как эти выражения достаточно громоздкие, они не приводятся в настоящих указаниях. Принеобходимости с ними можно ознакомиться по методическим указаниям [3].
Имеющиеся на вашей дискете процедуры метрического анализа механизма позволяют не только рассчитать передаточные функции, но и получить на экране дисплея изображение соответствующего структурного элемента, что необходимо для контроля правильности работы программы, а также наглядного представления о работе механизма и его особенностях.